
如图,AB为半圆O的直径,在AB的同侧作AC、BD切半圆O于A、B,CD切半圆O于E,请分别写出两个角相等、两条边相等、两个三角形全等、两个三角形相似等四个正确的结论.
①角相等:∠AOC=∠COE=∠BDO=∠EDO,∠ACO=∠ECO=∠DOE=∠DOB,
∠A=∠B=∠OEC=∠OED,
②边相等:AC=CE,DE=DB,OA=OB=OE;
③全等三角形:△OAC≌△OEC,△OBD≌△OED;
④相似三角形:△AOC∽△EOC∽△EDO∽△BDO∽△ODC.
【解析】
试题分析:根据切线的性质仔细分析图形即可判断.
由已知得:OA=OE,∠OAC=∠OEC,又OC公共,故△OAC≌OEC,
同理,△OBD ≌△OED,由此可得∠AOC=∠EOC,∠BOD=∠EOD,
从而∠COD="90°,∠AOC=∠BDO."
根据这些写如下结论:
①角相等:∠AOC=∠COE=∠BDO=∠EDO,∠ACO=∠ECO=∠DOE=∠DOB,
∠A=∠B=∠OEC=∠OED,
②边相等:AC=CE,DE=DB,OA=OB=OE;
③全等三角形:△OAC≌△OEC,△OBD≌△OED;
④相似三角形:△AOC∽△EOC∽△EDO∽△BDO∽△ODC.
考点:切线的性质
点评:切线的性质是圆中非常重要的知识点,是中考的热点,在各种题型中均有出现,一般难度不大,需多加注意.


科目:初中数学 来源: 题型:
 已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长.
已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长.查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学九年级下3.5直线和圆的位置关系练习卷(解析版) 题型:解答题
如图,AB是半圆O的直径,C为半圆上一点,过C作半圆的切线,连接AC, 作直线AD,使∠DAC=∠CAB,AD交半圆于E,交过C点的切线于点D.

(1)试判断AD与CD有何位置关系,并说明理由;
(2)若AB=10,AD=8,求AC的长.
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学九年级下3.3圆周角和圆心角的关系练习卷(解析版) 题型:解答题
如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tan∠BPD的值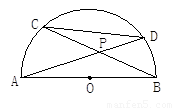
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com