
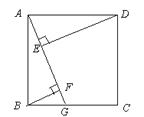
【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF;
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,并说明理由.
【答案】(1)证明见解析;(2)EF = 2FG,理由见解析.
【解析】分析:(1)本题的关键是求△ADE≌△ABF,以此来得出DE=AF=AE+EF=BE+EF,这两个三角形中已知的条件有AD=BA,一组直角,关键是再找出一组对应角相等,可通过证明∠DAF和∠ABF来实现.(通过平行和等角的余角相等来证得)
(2)通过证明△AFB ∽△BFG ∽△ABG,得出AB,BG;AF,BF;BF,BG之间的比例关系,根据点G为BC边中点,来得出AF,BF,BF,FG之间的比例关系,然后根据(1)中得出的结果来求BF,FG的大小关系.
详解:(1) 证明:
∵ 四边形ABCD 是正方形, BF⊥AG , DE⊥AG
∴ DA=AB, ∠BAF + ∠DAE = ∠DAE + ∠ADE = 90°
∴ ∠BAF = ∠ADE ∴ △ABF ≌ △DAE
∴ BF = AE , AF = DE
∴ DE-BF = AF-AE = EF
(2)EF = 2FG 理由如下:
∵ AB⊥BC , BF⊥AG , AB =2 BG
∴ △AFB ∽△BFG ∽△ABG
∴![]()
∴ AF = 2BF , BF =2FG
由(1)知, AE = BF,∴ EF = BF = 2 FG


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).
(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;
(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
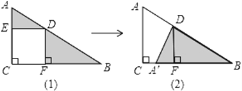
【题目】如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为_____.正方形EDFC的面积为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程mx2﹣(3m﹣1)x+2m﹣2=0
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2,且抛物线的开口向上时,求此抛物线的解析式;
(3)在坐标系中画出(2)中的函数图象,分析当直线y=x+b与(2)中的图象只有两个交点时b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,已知AD//BC,∠ABC=90°.

(1)若AC⊥BD,且AC=5,BD=3(如图1),求四边形ABCD的面积;
(2)若DE⊥BC于E,F是CD的中点,BD=BC,(如图2),求证:∠BAF=∠BCD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1.小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
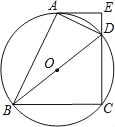
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com