
(2013•镇江模拟)已知圆锥的母线长OA=8,底面圆的半径为2,一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处,则小虫所走的最短距离为( )
A.8 B.4π C.8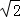 D.8
D.8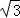
科目:初中数学 来源:2014-2015学年山东省临沂市九年级上学期基础学科竞赛数学试卷(解析版) 题型:填空题
已知A是反比例函数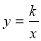 的图象上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是 .
的图象上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省东莞市八年级上学期期末考试数学试卷(解析版) 题型:解答题
观察下列等式:
?1×3+1=22
?3×5+1=42
?5×7+1=62
.......................................
请你按照上述三个等式的规律写出第④个、第⑤个等式;
请猜想,第n个等式(n为正整数)应表示为 ;
证明你猜想的结论.
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 14.2勾股定理的应用练习卷(解析版) 题型:?????
(2011•台湾)已知小龙、阿虎两人均在同一地点,若小龙向北直走160公尺,再向东直走80公尺后,可到神仙百货,则阿虎向西直走多少公尺后,他与神仙百货的距离为340公尺?( )
A.100 B.180 C.220 D.260
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 14.2勾股定理的应用练习卷(解析版) 题型:?????
(2014•邯郸二模)如图,圆柱底面半径为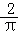 cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
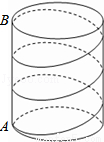
A.12cm B.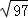 cm C.15cm D.
cm C.15cm D.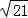 cm
cm
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 14.2勾股定理的应用练习卷(解析版) 题型:?????
(2014•龙东地区)一圆锥体形状的水晶饰品,母线长是10cm,底面圆的直径是5cm,点A为圆锥底面圆周上一点,从A点开始绕圆锥侧面缠一圈彩带回到A点,则彩带最少用多少厘米(接口处重合部分忽略不计)( )
A.10πcm B.10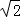 cm C.5πcm D.5
cm C.5πcm D.5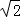 cm
cm
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.5逆命题与逆定理练习卷(解析版) 题型:?????
(2012•金东区一模)以下可以用来证明命题“任何偶数都是4的倍数”是假命题的反例为( )
A.3 B.4 C.8 D.6
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.1命题、定理与证明练习卷(解析版) 题型:?????
(2014•玉林)下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形
D.对角线垂直的平行四边形是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com