
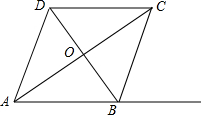
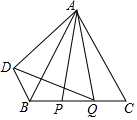
 已知:如图,菱形ABCD周长为20,对角线AC、BD交于点O,sin∠BAC=$\frac{3}{5}$.
已知:如图,菱形ABCD周长为20,对角线AC、BD交于点O,sin∠BAC=$\frac{3}{5}$.分析 (1)利用菱形的性质求出边长,再用三角函数求出OA,OB,即可得出AC,BD即可;
(2)先求出CF,BF,再分点Q在BC和CD上,两种情况用三角形面积公式即可得出和函数关系式;
(3)分点Q在CD和BC上,两种情况,判断出点Q的位置,根据点P的位置得出点P,Q运动时间,再求出点Q的运动路程,即可得出点Q的运动速度.
解答 解:(1)∵菱形ABCD周长为20,
∴AB=BC=CD=5,AC⊥BD,
在Rt△AOB中,sin∠BAC=$\frac{OB}{AB}$=$\frac{3}{5}$.
∴OB=3,
∴OA=4,
∴AC=2OA=8,BD=2OB=6,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×8=24,
(2)如图1,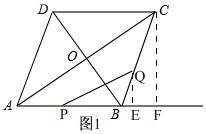 过点Q作QE⊥AB于E,过点C作CF⊥AB于F,
过点Q作QE⊥AB于E,过点C作CF⊥AB于F,
∴QE∥CF,
在Rt△ACF中,AC=8,sin∠BAC=$\frac{CF}{AC}$=$\frac{3}{5}$.
∴$\frac{CF}{8}=\frac{3}{5}$,
∴CF=$\frac{24}{5}$,
∴AF=$\frac{32}{5}$,
∴BF=AF-AB=$\frac{7}{5}$,
①当0<t<5时,
由运动知,AP=t,BQ=t,
∴BP=AB-AP=5-t,
∵QE∥CF,
∴△BEQ∽△BFC,
∴$\frac{BQ}{BC}=\frac{QE}{CF}$,
∴$\frac{t}{5}=\frac{QE}{\frac{24}{5}}$,
∴QE=$\frac{24}{25}$t,
∴S=S△PBQ=$\frac{1}{2}$BP•QE=$\frac{1}{2}$•(5-t)•$\frac{24}{25}$t=-$\frac{12}{25}{t}^{2}+\frac{12}{5}t$,
②当5<t≤10时,
如图2,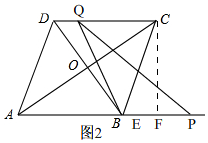 由运动知,AP=t,
由运动知,AP=t,
∴BP=AP-AB=t-5,
由①知,CF=$\frac{24}{5}$,
∴S=S△PBQ=$\frac{1}{2}$BP•CF=$\frac{1}{2}$•(t-5)•$\frac{24}{5}$=$\frac{12}{5}$(t-5)=$\frac{12}{5}$t-12.
∴$S=\left\{\begin{array}{l}{-\frac{12}{25}{t}^{2}+\frac{12}{5}t(0<t<5)}\\{\frac{12}{5}t-12(5<t≤10)}\end{array}\right.$;
(3)如图3,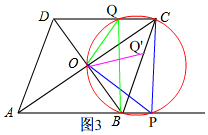 当点Q在CD上时,
当点Q在CD上时,
∵∠OQC+∠OBC=180°,
∴点O、B、C、Q四点共圆,
∵∠OQC+∠OBC=180°,∠OPC=∠OBC,
∴∠OQC+∠OPC=180°,
∴点O、P、C、Q四点共圆,
∴点O、B、P、C、Q五点共圆,
∴O、B、P、C四点共圆,
∴∠BPC+∠BOC=180°,
∵∠BOC=90°,
∴∠BPC=90°,
∵AB∥CD,
∴∠PCQ=90°,
同(2)①的方法得,BP=$\frac{7}{5}$,
∵点B、P、C、Q四点共圆,
∴∠BQC+∠BPC=180°,
∴∠CQB=90°,
∴四边形BPCQ是矩形,
∴CQ=BP=$\frac{7}{5}$,
∴AP=AB+BP=5+$\frac{7}{5}$=$\frac{32}{5}$,
∴t=$\frac{32}{5}$÷1=$\frac{32}{5}$,
∴BC+CQ=$\frac{32}{5}$,
∴$\frac{32}{5}$÷a=$\frac{32}{5}$,
∴a=1,
②当点Q在BC上时,
如图3中的Q',
∵OQC+∠OBC=180°,
∠OQ'C+∠OBC=180°,
∴∠OQC=∠OQ'C,
∵AC是菱形对角线,
∴∠OCQ=∠OCQ',
在△OCQ和△OCQ'中,$\left\{\begin{array}{l}{∠OQC=∠OQ'C}\\{∠OCQ=∠OCQ'}\\{OC=OC}\end{array}\right.$,
∴△OCQ≌△OCQ',
∴CQ'=CQ=$\frac{7}{5}$,
∴BQ'=BC-CQ'=$\frac{18}{5}$,
∴$\frac{18}{5}$÷a=$\frac{32}{5}$,
∴a=$\frac{9}{16}$,
即:满足条件的a的值为1或$\frac{9}{16}$.
点评 此题是四边形综合题,主要考查了菱形的性质,矩形的判定和性质,锐角三角函数,相似三角形的性质和判定,四点共圆,三角形的面积公式,全等三角形的判定和性质,求出点Q的运动路程是解本题的关键,考查的知识点比较多,是一道很好的中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
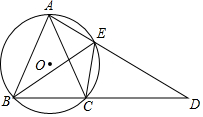 如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O交于点E,连接BE,CE.
如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O交于点E,连接BE,CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com