
| 次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
| 频数 | 16 | 25 | 9 | 7 | 3 |
分析 (1)将各组频数相加即可得;
(2)由频率分布表即可知组数和组距;
(3)将120≤x<180范围的两分组频数相加可得,再将其人数除以总人数即可得百分比.
解答 解:(1)全班有同学16+25+9+7+3=60(人);
(2)由频数分布表可知组距是90-60=30,组数是5;
(3)跳绳次数x在120≤x<180范围的同学有9+7=16人,占全班同学的$\frac{16}{60}$×100%≈26.7%.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.读图时要全面细致,同时,解题方法要灵活多样,切忌死记硬背,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
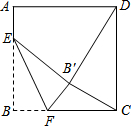 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com