
【题目】如图,反比例函数y=![]() 与反比例函数y=k2
与反比例函数y=k2![]() +b的图象的交点为A(m,1)、B(-2,n),OA与
+b的图象的交点为A(m,1)、B(-2,n),OA与![]() 轴正方向的夹角为α,且tanα=
轴正方向的夹角为α,且tanα=![]() 。
。
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值。
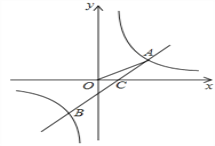
【答案】(1)直线AB的解析式为y=![]() x-1;(2)
x-1;(2)![]() .
.
【解析】试题分析:(1)用待定系数法求函数表达式,需要知道图像上点的坐标,根据![]() ,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入
,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入![]() ,求得反比例函数解析式
,求得反比例函数解析式![]() ,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式
,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式![]() ;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
试题解析:(1)过A作AE⊥x轴于E,∵tan∠AOE=tanα=![]() ,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数
,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数![]() 图像上,∴k1=4,∴反比例函数为
图像上,∴k1=4,∴反比例函数为![]() .∵B(-2,n)在反比例函数
.∵B(-2,n)在反比例函数![]() 图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得:
图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得: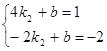 ,解得k2=
,解得k2=![]() ,b="-1," ∴直线AB的解析式为y=
,b="-1," ∴直线AB的解析式为y=![]() x-1;
x-1;
(2)∵直线AB的表达式为y=![]() x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
∴tanβ=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初二年级在元旦汇演中需要外出租用同一种服装若干件,已知在没有任何优惠的情况下,甲服装店租用2件和在乙服装店租用3件共需280元,在甲服装店租用4件和在乙服装店租用一件共需260元.
(1)求两个服装店提供的单价分别是多少?
(2)若该种服装提前一周订货则甲乙两个租售店都可以给予优惠,具体办法如下:甲服装店按原价的八折进行优惠;在乙服装店如果租用5件以上,且超出5件的部分可按原价的六折进行优惠;设需要租用x件服装,选择甲店则需要y1元,选择乙店则需要y2元,请分别求出y1,y2关于x的函数关系式;
(3)若租用的服装在5件以上,请问租用多少件时甲乙两店的租金相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出___只粽子,利润为___元;
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习同学们已经体会到灵活运用整式乘法公式给计算和化简带来的方便、快捷.相信通过下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.
例:用简便方法计算195×205.
解:195×205
=(200-5)(200+5) ①
=2002-52 ②
=39975.
(1)例题求解过程中,第②步变形是利用____________(填乘法公式的名称);
(2)用简便方法计算:
①9×11×101×10 001;
②(2+1)(22+1)(24+1)…(232+1)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4),乙看错了a,分解结果为(x+1)(x+9),则2a+b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM, 有4个结论:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,请将所有正确结论的序号填在横线上______.
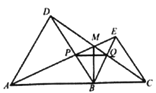
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com