
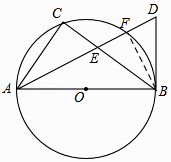
【题目】如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E. 
(1)求证:BD=BE;
(2)若DE=2,BD= ![]() ,求CE的长.
,求CE的长.
【答案】
(1)解:设∠BAD=α,
∵AD平分∠BAC
∴∠CAD=∠BAD=α,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠ABC=90°﹣2α,
∵BD是⊙O的切线,
∴BD⊥AB,
∴∠DBE=2α,
∠BED=∠BAD+∠ABC=90°﹣α,
∴∠D=180°﹣∠DBE﹣∠BED=90°﹣α,
∴∠D=∠BED,
∴BD=BE
(2)解:设AD交⊙O于点F,CE=x,则AC=2x,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵BD=BE,DE=2,
∴FE=FD=1,
∵BD= ![]() ,
,
∴tanα= ![]() ,
,
∴AB= ![]() =2
=2 ![]()
在Rt△ABC中,
由勾股定理可知:(2x)2+(x+ ![]() )2=(2
)2=(2 ![]() )2,
)2,
∴解得:x=﹣ ![]() 或x=
或x= ![]() ,
,
∴CE= ![]() ;
;
【解析】(1))设∠BAD=α,由于AD平分∠BAC,所以∠CAD=∠BAD=α,进而求出∠D=∠BED=90°﹣α,从而可知BD=BE;(2)设CE=x,由于AB是⊙O的直径,∠AFB=90°,又因为BD=BE,DE=2,FE=FD=1,由于BD= ![]() ,所以tanα=
,所以tanα= ![]() ,从而可求出AB=
,从而可求出AB= ![]() =2
=2 ![]() ,利用勾股定理列出方程即可求出x的值.
,利用勾股定理列出方程即可求出x的值.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE. 
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠PCB= ![]() ,BE=
,BE= ![]() ,求PF的长.
,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( ) 
A.∠2=35°
B.∠2=45°
C.∠2=55°
D.∠2=125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF= ![]() CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( ) 
A.6
B.4
C.7
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com