
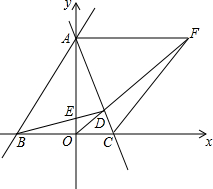
 如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由.
如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由. 分析 先根据勾股定理求出BE,再证明△OBE∽△DBC,得出比例式$\frac{OB}{BD}=\frac{BE}{BC}=\frac{OE}{DC}$,求出BD、DC,再由△AOC∽△BOE,得出比例式求出OA,证出△ABD是等腰直角三角形,得出AD=BD,然后由AF∥BC,证出△OCD∽△FAD,得出AF=OA,△AOF是等腰直角三角形,得出∠AOF=∠COF=45°,由△OKF≌△OCF,得出OK=OC=2,点K在y轴上,即可得出点K的坐标.
解答 解:存在,点K坐标为:0,2);理由如下:
∵B(-3,0)、C(2,0)、E(0,1),
∴OB=3,OC=2,OE=1,
∴BC=5,BE=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵BD⊥AC,
∴∠ADB=∠BDC=90°,
∵∠EBO=∠CBD,
∴△OBE∽△DBC,
∴$\frac{OB}{BD}=\frac{BE}{BC}=\frac{OE}{DC}$,
即$\frac{3}{BD}=\frac{\sqrt{10}}{5}=\frac{1}{DC}$,
∴BD=$\frac{3\sqrt{10}}{2}$,DC=$\frac{\sqrt{10}}{2}$,
∵∠AOC=∠BOE=90°,
∴∠OAC+∠OCA=90°,∠EBO+∠OCA=90°,
∴∠OAC=∠EBO,
∴△AOC∽△BOE,
∴$\frac{OA}{OB}=\frac{OC}{OE}$=$\frac{2}{1}$,
∴OA=2OB=6,
∵∠BAC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD=$\frac{3\sqrt{10}}{2}$,
∵AF∥BC,
∴∠OAF=∠AOB=90°,△OCD∽△FAD,
∴$\frac{OC}{AF}=\frac{DC}{AD}$=$\frac{1}{3}$,
∴AF=3OC=6,
∴OA=AF,
∴∠AOF=∠AFO=45°,
∴∠COF=45°,
∵△OKF≌△OCF,
∴OK=OC=2,点K在y轴上,
∴点K的坐标为:(0,2).
点评 本题是一次函数综合题目,考查了坐标与图形特征、勾股定理、相似三角形的判定与性质、等腰直角三角形的判定与性质等知识,本题难度较大,综合性强,需要证明三角形相似得出比例式和等腰直角三角形才能得出结果.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
 每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$)
每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
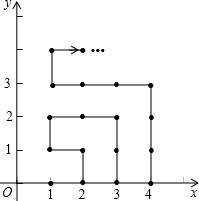 在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中→方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2)…那么第23个点是多少?
在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中→方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2)…那么第23个点是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
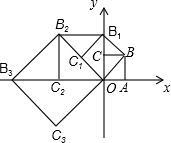 如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0).
如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com