
三个小球上分别标有-2,0,1三个数,这三个球除了标的数不同外,其余均相同.将
小球放入一个不透明的布袋中搅匀.
(1)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸
出一个小球,再记下小球上所标之数.求两次记下之数的和大于0的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,将小球上所标之数再记下,…,这样一共摸了13次.若记下的13个数之和等于-4,平方和等于14,求:这13次摸球中,摸到球上所标之数是0的次数.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
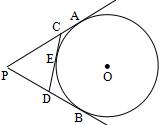
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E交PA、PB于C、D,若⊙O的半径为r,PCD的周长等于3r,则tan∠APB的值是( )
A.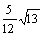 B.
B.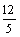
C.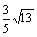 D.
D.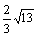
查看答案和解析>>
科目:初中数学 来源: 题型:
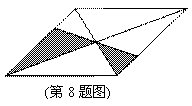
小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖
落在阴影区域的概率是( )
A.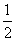 B.
B.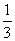 C.
C.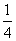 D.
D.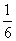
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
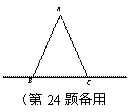
【探究发现】如图1, 是等边三角形,
是等边三角形, ,EF交等边三角形外角平分线CF所在的直线于点F.当点E是BC的中点时,有AE=EF成立;
,EF交等边三角形外角平分线CF所在的直线于点F.当点E是BC的中点时,有AE=EF成立;
【数学思考】某数学兴趣小组在探究AE、EF的关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:当点E是直线BC上(B,C除外)任意一点时(其它条件不变),结论AE=EF仍然成立.
假如你是该兴趣小组中的一员,请你从“点E是线段BC上的任 意一点”;“点E是线段BC延长线上的任意一点”;“ 点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在备用图1中画出图形,并进行证明.
意一点”;“点E是线段BC延长线上的任意一点”;“ 点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在备用图1中画出图形,并进行证明.
 | |||
 | |||

【拓展应用】当点E在线段BC的延长线上时,若CE = BC,在备用图2中画出图形,并运用上述结论求出 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=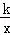 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
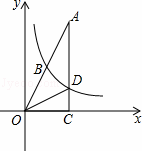
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com