
【题目】已知:关于x、y的方程组![]() 的解为非负数.
的解为非负数.
(1)求a的取值范围;
(2)化简|2a+4|﹣|a﹣1|;
(3)在a的取值范围内,a为何整数时,使得2ax+3x<2a+3解集为x>1.
【答案】(1)﹣2≤a≤﹣1;(2)3a+3;(3)在a的取值范围内,a=﹣2时,使得2ax+3x<2a+3解集为x>1.
【解析】
(1)先解方程组,根据解为非负数,得出a的取值范围;
(2)根据a的取值范围化简|2a+4|﹣|a﹣1|即可;
(3)根据2ax+3x<2a+3解集为x>1,得出a的值即可.
(1)由![]() .
.
∵方程组![]() 的解为非负数,∴
的解为非负数,∴![]() ,得:﹣2≤a≤﹣1;
,得:﹣2≤a≤﹣1;
(2)∵﹣2≤a≤﹣1,∴|2a+4|﹣|a﹣1|=2a+4﹣(1﹣a)=2a+4﹣1+a=3a+3;
(3)∵2ax+3x<2a+3解集为x>1,∴2a+3<0,∴a<-1.5.
∵﹣2≤a≤﹣1,∴若a为整数,则a=﹣2,即在a的取值范围内,a=﹣2时,使得2ax+3x<2a+3解集为x>1.


科目:初中数学 来源: 题型:
【题目】如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值![]() , 则满足条件的不全等的“圆环带”有( )
, 则满足条件的不全等的“圆环带”有( )
A.1个
B.2个
C.3个
D.无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.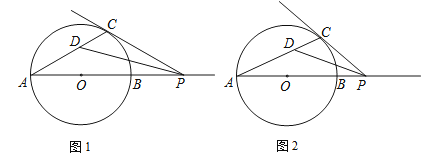
(1)如图1,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图2,若点P位于(1)中不同的位置,(1)的结论是否仍然成立?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,求∠FEB的度数.

(2)如图,A地和B地都是海上观测站,从A地发现它的北偏东60方向有一艘船P,同时,从B地发现这艘船P在它北偏东30方向.试在图中画出这艘船P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB中,半径OA=2,∠AOB=120°,C是 ![]() 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( ) 
A.![]() ﹣2
﹣2 ![]()
B.![]() ﹣2
﹣2 ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
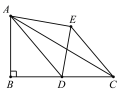
【题目】如图,在Rt△ABC中,AB=3,BC=8,点D为BC的中点,将△ABD沿AD折叠,使点B落在点E处,连接CE,则CE的长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com