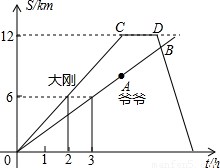
解:(1)设S
1=k
1t,
∵点(2,6)在S
1=k
1t图象上,
∴6=2k
1,
解得:k
1=3,
∴大刚行进的路程S
1(km)与时间t(h)的函数关系式为:S
1=3t;
设S
2=k
2t,
∵点(3,6)在S
2=k
2t图象上,
∴6=3k
2,
解得:k
2=2,
∴爷爷行进的路程S
2(km)与时间t(h)的函数关系式为S
2=2t.
(2)∵大刚到达山顶所用时间为:
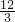
=4(h),
此时S
2=8,12-8=4(km),
即爷爷距山顶的距离为4km.
(3)∵点B与山顶的距离为1.5km,
∴爷爷从山脚到达点B的路程=12-1.5=10.5km,
∴爷爷从山脚到达点B所用的时间为:10.5÷2=
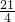
(h),
∴大刚到达B处用时:5.25-5=0.25(h),
∴大刚下山时的速度是:
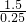
=6(km/h).
∴大刚下山时的速度是6km/h.
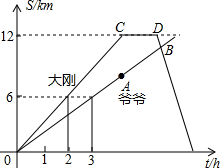
分析:(1)观察图象可得大刚行进的路程S
1(km)与时间t(h)的关系与爷爷行进的路程S
2(km)与时间t(h)的函数关系式都是正比例函数,然后根据待定系数法求解即可求得答案;
(2)首先根据函数关系式S
1=3t求得大刚到达山顶所用时间,然后代入S
2=2t,求得爷爷行进的路程,继而可求得点A距山顶的距离;
(3)首先根据题意可求得大刚到达B处用时,利用:速度=

,即可求得大刚下山时的速度.
点评:此题考查了一次函数的实际应用问题.此题难度适中,解题的关键是根据题意利用待定系数法求得函数解析式,然后利用一次函数解实际问题.

 km的B处与爷爷相遇,求大刚下山时的速度.
km的B处与爷爷相遇,求大刚下山时的速度.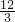 =4(h),
=4(h),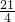 (h),
(h),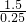 =6(km/h).
=6(km/h). ,即可求得大刚下山时的速度.
,即可求得大刚下山时的速度.

 km的B处与爷爷相遇,求大刚下山时的速度.
km的B处与爷爷相遇,求大刚下山时的速度.