
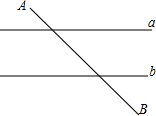
 如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=2$\sqrt{30}$.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=8.
如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=2$\sqrt{30}$.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=8. 分析 MN表示直线a与直线b之间的距离,是定值,只要满足AM+NB的值最小即可.过A作直线a的垂线,并在此垂线上取点A′,使得AA′=MN,连接A'B,则A'B与直线b的交点即为N,过N作MN⊥a于点M.则A'B为所求,利用勾股定理可求得其值.
解答 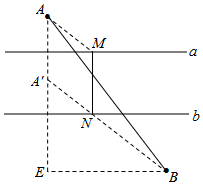 解:过A作直线a的垂线,并在此垂线上取点A′,使得AA′=4,连接A′B,与直线b交于点N,过M作直线a的垂线,交直线a于点N,连接AN,过点B作BE⊥AA′,交射线AA′于点E,如图.
解:过A作直线a的垂线,并在此垂线上取点A′,使得AA′=4,连接A′B,与直线b交于点N,过M作直线a的垂线,交直线a于点N,连接AN,过点B作BE⊥AA′,交射线AA′于点E,如图.
∵AA′⊥a,MN⊥a,
∴AA′∥MN.
又∵AA′=MN=4,
∴四边形AA′NM是平行四边形,
∴AM=A′N.
由于AM+MN+NB要最小,且MN固定为4,所以AM+NB最小.
由两点之间线段最短,可知AM+NB的最小值为A′B.
∵AE=2+3+4=9,AB=$2\sqrt{30}$,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{39}$,
∵A′E=AE-AA′=9-4=5,
∴A′B=$\sqrt{A′{E}^{2}+B{E}^{2}}$=8
所以AM+NB的最小值为8.
故答案为:8.
点评 本题考查了轴对称-最小距离问题,勾股定理的应用、平行线之间的距离,解答本题的关键是找到点M、点N的位置,难度较大,注意掌握两点之间线段最短.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)2015×1=-1 | B. | (-3)2=-9 | C. | -(-8)=-8 | D. | (-6)÷3×(-$\frac{1}{3}$)=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-1)2 | B. | y=x2-1 | C. | y=(x+1)2 | D. | y=x2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000(1+x)2=3500 | B. | 1000(1+x)+1000(1+x)2=2500 | ||
| C. | 1000(1+x)+1000(1+x)2=3500 | D. | 1000(1+x)2=2500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=x2-2x-3 | … | 5 | 0 | -3 | -4 | -3 | 0 | 5 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com