
ЁОЬтФПЁПЖЈвхЃКгавЛзщЖдБпгывЛЬѕЖдНЧЯпОљЯрЕШЕФЫФБпаЮЮЊЖдЕШЫФБпаЮЃЌетЬѕЖдНЧЯпгжГЦЖдЕШЯпЃЎ
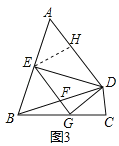
ЃЈ1ЃЉШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌЁЯCЃНЁЯBDCЃЌEЮЊABЕФжаЕуЃЌDEЁЭABЃЎЧѓжЄЃКЫФБпаЮABCDЪЧЖдЕШЫФБпаЮЃЎ
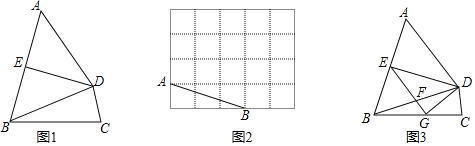
ЃЈ2ЃЉШчЭМ2ЃЌдк5ЁС4ЕФЗНИёжНжаЃЌAЃЌBдкИёЕуЩЯЃЌЧыЛГівЛИіЗћКЯЬѕМўЕФЖдЕШЫФБпаЮABCDЃЌЪЙBDЪЧЖдЕШЯпЃЌCЃЌDдкИёЕуЩЯЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌдкЭМЃЈ1ЃЉЕФЬѕМўЯТЃЌЙ§ЕуEзїADЕФЦНааЯпНЛBDЃЌBCгкЕуFЃЌGЃЌСЌНсDGЃЌШєDGЁЭEGЃЌDGЃН2ЃЌABЃН5ЃЌЧѓЖдЕШЯпBDЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉBDЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЫЕУїЁЯC=ЁЯBDCЃЌжЄЕУBC=BDЃЌШЛКѓгЩЕШбќШ§НЧаЮЕФаджЪЕУЕНBD=ADЃЌМДПЩжЄУїЃЛ
ЃЈ2ЃЉзїA BЕФДЙжБЦНЗжЯпгыЗНИёжНЩЯЕФИёЕуЕФНЛЕуМДЮЊЕуDЃЌдйвдЕуBЮЊдВаФЁЂвдBDГЄЮЊАыОЖЛдВЃЌдВгыЗНИёжНЩЯЕФИёЕуЕФНЛЕуМДЮЊЕуCЃЌСЌНгADЁЂBCЁЂCDЃЌдђAD=BC=BDМДПЩЭъГЩзїЭМЃЛ
ЃЈ3ЃЉЙ§ЕуEзїEHЁЭADгкHЃЌЯШжЄЕУЫФБпаЮDGEHЪЧОиаЮЃЌЕУГіEH=DG=2ЃЛШЛКѓдйЧѓГіAEЕФГЄЃЛЃЌSЁїADE=SЁїBDEЃЌЩшDE=xЃЌA D=BD=yЃЌШЛКѓдйдЫгУЙДЙЩЖЈРэКЭШ§НЧаЮЕФУцЛ§ЙЋЪНСаГіЗНГЬзщЧѓНтМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКЁпЁЯCЃНЁЯBDCЃЌ
ЁрBCЃНBDЃЌ
ЁпEЮЊABЕФжаЕуЃЌDEЁЭABЃЌ
ЁрBDЃНADЃЌ
ЁрBCЃНADЃНBDЃЌ
ЁрЫФБпаЮABCDЪЧЖдЕШЫФБпаЮЃЛ
ЃЈ2ЃЉНтЃКгаСНжжЛЗЈЃК
зїABЕФДЙжБЦНЗжЯпгыЗНИёжНЩЯЕФИёЕуЕФНЛЕуМДЮЊЕуDЃЌдйвдЕуBЮЊдВаФЁЂвдBDГЄЮЊАыОЖЛдВЃЌдВгыЗНИёжНЩЯЕФИёЕуЕФНЛЕуМДЮЊЕуCЃЌСЌНгADЁЂBCЁЂCDЃЌдђADЃНBCЃНBDЃЌШчЭМ2Љ1ЫљЪОЃЛ
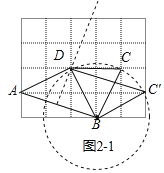
ЃЈ3ЃЉНтЃКЙ§ЕуEзїEHЁЭADгкHЃЌШчЭМ3ЫљЪОЃК
дђЁЯEHDЃН90ЁуЃЌ
ЁпEGЁЮADЃЌDGЁЭEGЃЌ
ЁрЁЯEGDЃНЁЯHDGЃН90ЁуЃЌ
ЁрЫФБпаЮDGEHЪЧОиаЮЃЌ
ЁрEHЃНDGЃН2ЃЌ
ЁпEЮЊABЕФжаЕуЃЌABЃН5ЃЌ
ЁрAEЃНBEЃН![]() ABЃН
ABЃН![]() ЃЌSЁїADEЃНSЁїBDEЃЌ
ЃЌSЁїADEЃНSЁїBDEЃЌ
ЩшDEЃНxЃЌADЃНBDЃНyЃЌ
дђSЁїADEЃН![]() EHADЃН
EHADЃН![]() ЁС2ЁСyЃНyЃЌSЁїBDEЃН
ЁС2ЁСyЃНyЃЌSЁїBDEЃН![]() BEDEЃН
BEDEЃН![]() ЁС
ЁС![]() ЁСxЃН
ЁСxЃН![]() xЃЌ
xЃЌ
ЁпдкRtЁїBDEжаЃЌЁЯBEDЃН90ЁуЃЌ
ЁрBD2ЃНBE2+DE2ЃЌМДy2ЃНЃЈ![]() ЃЉ2+x2ЃЌ
ЃЉ2+x2ЃЌ
Ёр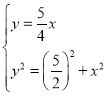 ЃЌ
ЃЌ
НтЕУЃК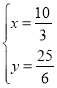
ЁрBDЃН![]() ЃЎ
ЃЎ


 НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛЖЮХзЮяЯпЃК![]() МЧЮЊ
МЧЮЊ![]() ЃЌЫќгы
ЃЌЫќгы![]() жсНЛгкСНЕу
жсНЛгкСНЕу![]() ЃЌ
ЃЌ![]() ЃЛНЋ
ЃЛНЋ![]() ШЦ
ШЦ![]() а§зЊ180ЁуЕУЕН
а§зЊ180ЁуЕУЕН![]() ЃЌНЛ
ЃЌНЛ![]() жсгк
жсгк![]() ЃЛНЋ
ЃЛНЋ![]() ШЦ
ШЦ![]() а§зЊ180ЁуЕУЕН
а§зЊ180ЁуЕУЕН![]() ЃЌНЛ
ЃЌНЛ![]() жсгк
жсгк![]() ШчДЫБфЛЛНјааЯТШЅЃЌШєЕу
ШчДЫБфЛЛНјааЯТШЅЃЌШєЕу![]() дкетжжСЌајБфЛЛЕФЭМЯѓЩЯЃЌдђ
дкетжжСЌајБфЛЛЕФЭМЯѓЩЯЃЌдђ![]() ЕФжЕЮЊЃЈ ЃЉ
ЕФжЕЮЊЃЈ ЃЉ
A.2B.3C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊШЋУцЭЦНјЁАШ§ЙЉвЛвЕЁБЗжРывЦНЛЙЄзїЃЌМзЁЂввСНИіЙЄГЬЖгГаРПСЫФГЩчЧј2400УзЕФЕчТЗЙмЕРЦЬЩшЙЄГЬЃЎвбжЊМзЖгУПЬьЦЬЩшЙмЕРЕФГЄЖШЪЧввЖгУПЬьЦЬЩшЙмЕРГЄЖШЕФ1ЃЎ5БЖЃЌШєСНЖгИїздЖРСЂЭъГЩ1200УзЕФЦЬЩшШЮЮёЃЌдђМзЖгБШввЖгЩйгУ10ЬьЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНЙЄГЬЖгУПЬьЗжБ№ЦЬЩшЕчТЗЙмЕРЖрЩйУзЃЛ
ЃЈ2ЃЉШєМзЖгВЮгыИУЯюЙЄГЬЕФЪЉЙЄЪБМфВЛЕУГЌЙ§20ЬьЃЌдђввЖгжСЩйЪЉЙЄЖрЩйЬьВХФмЭъГЩИУЯюЙЄГЬЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
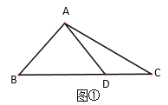
ЁОЬтФПЁПЃЈЮЪЬтЬНОПЃЉПЮЬУЩЯРЯЪІЬсГіСЫетбљЕФЮЪЬтЃКЁАШчЭМЂйЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() БпЩЯЕФвЛЕуЃЌ
БпЩЯЕФвЛЕуЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЁБЃЎФГЭЌбЇзіСЫШчЯТЕФЫМПМЃКШчЭМЂкЃЌЙ§Еу
ЕФГЄЁБЃЎФГЭЌбЇзіСЫШчЯТЕФЫМПМЃКШчЭМЂкЃЌЙ§Еу![]() зї
зї![]() ЃЌНЛ
ЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌНјЖјЧѓНтЃЌЧыЛиД№ЯТСаЮЪЬтЃК
ЃЌНјЖјЧѓНтЃЌЧыЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() ___________ЖШЃЛ
___________ЖШЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
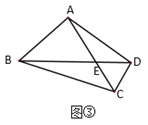
ЃЈЭиеЙгІгУЃЉШчЭМЂлЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЖдНЧЯп
ЃЌЖдНЧЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊ_____________ЃЎ
ЕФГЄЮЊ_____________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
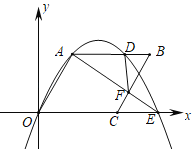
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮOABCЕФБпГЄЮЊ2ЃЌЁЯAOCЃН60ЁуЃЌЕуDЮЊABБпЩЯЕФвЛЕуЃЌОЙ§OЃЌAЃЌDШ§ЕуЕФХзЮяЯпгыxжсЕФе§АыжсНЛгкЕуEЃЌСЌНсAEНЛBCгкЕуFЃЌЕБDFЁЭABЪБЃЌCEЕФГЄЮЊ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ![]() ФквЛЕуЃЌЧв
ФквЛЕуЃЌЧв![]() ЃЌдђ
ЃЌдђ![]() ЕФзюаЁжЕЮЊ______ЃЎ
ЕФзюаЁжЕЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЕу
ЃЎЕу![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЩЯЕФЖЏЕуЃЌСЌНг
ЩЯЕФЖЏЕуЃЌСЌНг![]() ЃЎЩш
ЃЎЩш![]() ЃЈ
ЃЈ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕШчЭМЂкЫљЪОЃЎ
жЎМфЕФКЏЪ§ЙиЯЕШчЭМЂкЫљЪОЃЎ
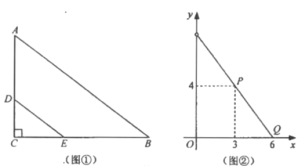
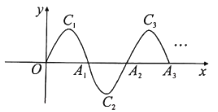
ЃЈ1ЃЉЧѓГіЭМЂкжаЯпЖЮ![]() ЫљдкжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЫљдкжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉНЋ![]() би
би![]() ЗелЃЌЕУ
ЗелЃЌЕУ![]() ЃЎ
ЃЎ
ЂйЕу![]() ЪЧЗёПЩвдТфдк
ЪЧЗёПЩвдТфдк![]() ЕФФГЬѕНЧЦНЗжЯпЩЯ?ШчЙћПЩвдЃЌЧѓГіЯргІ
ЕФФГЬѕНЧЦНЗжЯпЩЯ?ШчЙћПЩвдЃЌЧѓГіЯргІ![]() ЕФжЕЃЛШчЙћВЛПЩвдЃЌЫЕУїРэгЩЃЛ
ЕФжЕЃЛШчЙћВЛПЩвдЃЌЫЕУїРэгЩЃЛ
ЂкжБНгаДГі![]() гы
гы![]() жиЕўВПЗжУцЛ§ЕФзюДѓжЕМАЯргІ
жиЕўВПЗжУцЛ§ЕФзюДѓжЕМАЯргІ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
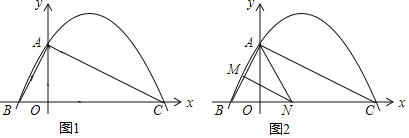
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЖўДЮКЏЪ§y=ax2+![]() x+cЃЈaЁй0ЃЉЕФЭМЯѓгыyжсНЛгкЕуAЃЈ0ЃЌ4ЃЉЃЌгыxжсНЛгкЕуBЁЂCЃЌЕуCзјБъЮЊЃЈ8ЃЌ0ЃЉЃЌСЌНгABЁЂACЃЎ
x+cЃЈaЁй0ЃЉЕФЭМЯѓгыyжсНЛгкЕуAЃЈ0ЃЌ4ЃЉЃЌгыxжсНЛгкЕуBЁЂCЃЌЕуCзјБъЮЊЃЈ8ЃЌ0ЃЉЃЌСЌНгABЁЂACЃЎ
ЃЈ1ЃЉЧыжБНгаДГіЖўДЮКЏЪ§y=ax2+![]() x+cЕФБэДяЪНЃЛ
x+cЕФБэДяЪНЃЛ
ЃЈ2ЃЉХаЖЯЁїABCЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуNдкxжсЩЯдЫЖЏЃЌЕБвдЕуAЁЂNЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЪБЃЌЧыаДГіДЫЪБЕуNЕФзјБъЃЛ
ЃЈ4ЃЉШчЭМ2ЃЌШєЕуNдкЯпЖЮBCЩЯдЫЖЏЃЈВЛгыЕуBЁЂCжиКЯЃЉЃЌЙ§ЕуNзїNMЁЮACЃЌНЛABгкЕуMЃЌЕБЁїAMNУцЛ§зюДѓЪБЃЌЧѓДЫЪБЕуNЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
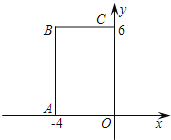
ЁОЬтФПЁП ШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуOдкзјБъдЕуЃЌБпOAдкxжсЩЯЃЌ
OCдкyжсЩЯЃЌШчЙћОиаЮOAЁфBЁфCЁфгыОиаЮOABCЙигкЕуOЮЛЫЦЃЌЧвОиаЮOAЁфBЁфCЁфЕФУцЛ§ЕШгкОиаЮOABCУцЛ§ЕФ![]() ЃЌФЧУДЕуBЁфЕФзјБъЪЧЁО ЁП
ЃЌФЧУДЕуBЁфЕФзјБъЪЧЁО ЁП
AЃЎЃЈЃ2ЃЌ3ЃЉ BЃЎЃЈ2ЃЌЃ3ЃЉ CЃЎЃЈ3ЃЌЃ2ЃЉЛђЃЈЃ2ЃЌ3ЃЉ DЃЎЃЈЃ2ЃЌ3ЃЉЛђЃЈ2ЃЌЃ3ЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com