

分析 (1)先判断出MA=MD,∠A=∠D=90°,AB=DC即可判断出结论;
(2)先判断出四边形MENF是平行四边形,再判断出ME=MF即可得出结论;
(3)先判断出∠AMB+∠DMC=90°,进而判断出∠AMB=∠ABM=45°,即可得出AB=AM,即可得出结论.
解答 解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,
∵M是边AD的中点,
∴MA=MD,
在△ABM和△DCM中,$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠B}\\{MA=MD}\end{array}\right.$,
∴△ABM≌△DCM;
(2)四边形MENF是菱形;
理由:∵N,E,F分别是BC,BM,CM的中点,
∴NE∥CM,NE=$\frac{1}{2}$CM,MF=$\frac{1}{2}$CM,
∴NE=FM,
∵NE∥FM,
∴四边形MENF是平行四边形,
由(1)知,△ABM≌△DCM,
∴BM=CM,
∵E,F分别是BM、CM的中点,
∴ME=$\frac{1}{2}$BM,MF=$\frac{1}{2}$CM,
∴ME=MF,
∴?MENF是菱形;
(3)∵四边形NEMF是正方形,
∴∠EMF=90°,
∴∠AMB+∠DMC=90°,
由(1)知,△ABM≌△DCM,
∴∠AMB=∠DMC,
∴∠AMB=45°,
在△ABM中,∠ABM=90°-45°=45°,
∴AB=AM,
∵M是AD的中点,
∴AD=2AM,
∴AD=2AB,
∴AD:AB=2:1,
故答案为2:1.
点评 此题是四边形综合题,主要考查了矩形的性质,平行四边形的判定和性质,菱形的判定,正方形的性质,全等三角形的判定和性质,解(1)的关键是判断出MA=MD,解(2)的关键是判断出四边形MENF是平行四边形,解(3)的关键是判断出∠AMB=∠ABM=45°.


科目:初中数学 来源: 题型:选择题
| A. | x2-2x+1=(x-1)2 | B. | (x+1)(x-1)=x2-1 | C. | x2-2x+1=x(x-2)+1 | D. | (x+3)(x-2)=x2+x-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
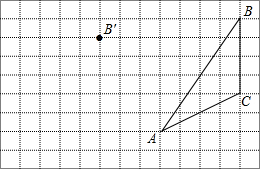 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某同学想用一块面积为400cm2的正方形纸片,(如图所示)沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,请你用所学过的知识来说明能否用这块纸片裁出符合要求的纸片.
某同学想用一块面积为400cm2的正方形纸片,(如图所示)沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,请你用所学过的知识来说明能否用这块纸片裁出符合要求的纸片.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com