
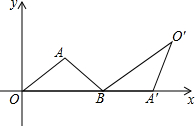
 如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$.
如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$. 分析 如图作AF⊥OB于F,O′E⊥OB于E,由cos∠ABF=cos∠EBO′得$\frac{BF}{AB}$=$\frac{BE}{BO′}$,求出BE即可解决问题.
解答 解:如图作AF⊥OB于F,O′E⊥OB于E,
∵OA=AB=6,AF⊥OB,
∴OF=FB=5,
∵cos∠ABF=cos∠EBO′,
∴$\frac{BF}{AB}$=$\frac{BE}{BO′}$,
∴$\frac{5}{6}$=$\frac{BE}{10}$,
∴BE=$\frac{25}{3}$,
∴OE=10+$\frac{25}{3}$=$\frac{55}{3}$,
∴点O′的横坐标为$\frac{55}{3}$.
点评 本题考查坐标与图形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形,属于中考常考题型.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
 为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.
为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
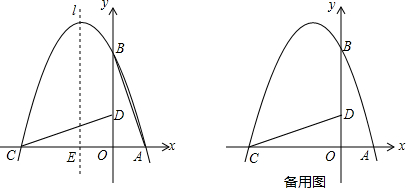
 如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com