
 如图,在平面直角坐标系中,Rt△ABO的顶点A、B的坐标分别为(3,0)、(0,1),点D、E是AO的三等分点,且点D在点E的右侧,点F是AB的中点.动点P从点B出发,以每秒$\sqrt{2}$个单位长度的速度沿折线BE-EF-FD运动.当点P不与点E、F重合时,过点P作其运动所在线段的垂线,交AB边于点N,交BO或AO于点M.设点P运动时间为t(秒).
如图,在平面直角坐标系中,Rt△ABO的顶点A、B的坐标分别为(3,0)、(0,1),点D、E是AO的三等分点,且点D在点E的右侧,点F是AB的中点.动点P从点B出发,以每秒$\sqrt{2}$个单位长度的速度沿折线BE-EF-FD运动.当点P不与点E、F重合时,过点P作其运动所在线段的垂线,交AB边于点N,交BO或AO于点M.设点P运动时间为t(秒).分析 (1)根据A、B坐标,中位线性质,易得F的坐标;利用等腰直角三角形判定,易得∠FDG=45°,从而判断出△DEF的形状;
(2)利用分类讨论思想,当过点O且垂直与BE时,t=$\frac{1}{2}$;若点P与E重合时,t=1;利用三角形相似,表示出线段长度;
(3)利用分类讨论思想,四边形的面积公式,分当P在线段EF上时;当P在线段FD上时;数形结合,得出答案;
(4)分别利用平行四边形的判定与性质以及全等三角形的判定与性质结合,当0≤t<$\frac{1}{2}$时;当$\frac{1}{2}$≤t<1时;当1≤t<$\frac{3}{2}$时;当$\frac{3}{2}$≤t<2时;分别得出符合题意的答案即可.
解答 解:(1)F($\frac{3}{2}$,$\frac{1}{2}$);
如图1,过F做AO的垂线,垂足为G,
∵FG=$\frac{1}{2}$OB=$\frac{1}{2}$,
EG=DG=$\frac{1}{2}$ED=$\frac{1}{2}$=FG,
∴△EFD为等腰直角三角形;
(2)①当0≤t<$\frac{1}{2}$时,如图2,
∵$\frac{BP}{BE}$=$\frac{NP}{EF}$,即$\frac{\sqrt{2}t}{\sqrt{2}}$=$\frac{NP}{\frac{\sqrt{2}}{2}}$,
∴NP=$\frac{\sqrt{2}}{2}$t,
∵MP=BP=$\sqrt{2}$t,
∴MN=$\frac{3\sqrt{2}}{2}$t;
②当$\frac{1}{2}$≤t<1时,如图3,
∵NP=$\frac{\sqrt{2}}{2}$t,MP=PE=$\sqrt{2}$$-\sqrt{2}$t,
∴MN=NP+MP=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t;
(3)当P在线段EF上时,如图4,
∵PF=$\frac{3\sqrt{2}}{2}$-$\sqrt{2}$t,
∴NP=2PF=$3\sqrt{2}$-$2\sqrt{2}$t,
∵PE=$\sqrt{2}$t-$\sqrt{2}$=PM;
∴MN=$2\sqrt{2}$-$\sqrt{2}$t,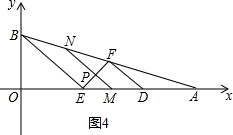
EF=$\frac{\sqrt{2}}{2}$,
∴S四边形EFMN=$\frac{1}{2}$EF•MN=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×($2\sqrt{2}$-$\sqrt{2}$t)=$\frac{2-t}{2}$;
当P在线段FD上时,如图5,
∵PF=$\sqrt{2}t-\frac{3}{2}\sqrt{2}$,
∴NP=$\frac{1}{2}$PF=$\frac{\sqrt{2}}{2}$t-$\frac{3}{4}$$\sqrt{2}$, PD=$\frac{\sqrt{2}}{2}$-($\sqrt{2}$t-$\sqrt{2}$-$\frac{\sqrt{2}}{2}$)=$2\sqrt{2}$-$\sqrt{2}$t,
PD=$\frac{\sqrt{2}}{2}$-($\sqrt{2}$t-$\sqrt{2}$-$\frac{\sqrt{2}}{2}$)=$2\sqrt{2}$-$\sqrt{2}$t,
PM=PD=$2\sqrt{2}$-$\sqrt{2}$t,
∴S四边形EFMN=$\frac{1}{2}$(MN+EF)•PF=-t2+$\frac{13}{4}$t-$\frac{21}{8}$;
(4)①如图6,
连接ME,作FQ⊥AO于点Q,当0≤t<$\frac{1}{2}$时, ∵OB=EO=1,
∵OB=EO=1,
∴∠BEO=45°,
∵F为AB的中点,FQ∥BO,
∴Q为AO的中点,
∴FQ=EQ=$\frac{1}{2}$,
∴∠EFQ=45°,
∴BE⊥EF,
∴MN∥EF,
当ME∥AB时,
故四边形NMEF是平行四边形,
则有两对角对应相等,
∵ME∥AB,
∴△OME∽△OBA,
∴$\frac{OM}{OB}$=$\frac{OE}{AO}$=$\frac{1}{3}$,
∴BM=$\frac{2}{3}$,
∴BP=$\frac{\sqrt{2}}{2}$BM=$\frac{\sqrt{2}}{3}$,
∵P以每秒$\sqrt{2}$个单位长度的速度沿折线BE-EF-FD运动,
∴t=$\frac{\sqrt{2}}{3}$÷$\sqrt{2}$=$\frac{1}{3}$(s),
即当t=$\frac{1}{3}$s时,四边形MEFN是平行四边形,一定有一组对角相等;
②当$\frac{1}{2}$≤t<1时,MN≠EF,不存在,以M、N、E、F为顶点的四边形存在一组对角相等;
③如图7,
当1≤t<$\frac{3}{2}$时,当MN垂直平分EF,此时NE=NF,EM=FM,
在△NEM和△NFM中,
$\left\{\begin{array}{l}{NE=NF}\\{MN=MN}\\{EM=FM}\end{array}\right.$,
∴△NEM≌△NFM(SSS),
∴∠NEM=∠NFD,
∵FM=EM=$\frac{1}{2}$,
∴EF=$\frac{\sqrt{2}}{2}$,
此时EP=$\frac{1}{2}$EF=$\frac{\sqrt{2}}{4}$,
即当t=$\frac{\sqrt{2}}{4}$÷$\sqrt{2}$=$\frac{1}{4}$(s)时,四边形MEFN,一定有一组对角相等;
④当$\frac{3}{2}$≤t<2时,MN≠EF,不存在,以M、N、E、F为顶点的四边形存在一组对角相等.
点评 此题主要考查了相似三角形的判定与性质以及全等三角形的判定与性质额平行四边形的判定与性质等知识,利用分类讨论以及数形结合得出是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,A(1,4),B(3,1)
如图,平面直角坐标系中,A(1,4),B(3,1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
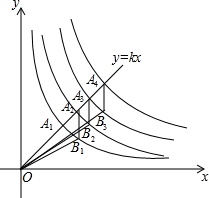 如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )
如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )| A. | 1007 | B. | $\frac{2013}{2}$ | C. | 1006 | D. | $\frac{2011}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b | B. | a=b | C. | a<b | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1:y=kx+b与x轴交于点B(1,0),直线l2:$y=\frac{1}{2}x+1$与y轴交于点C,这两条直线交于点A(2,a).
如图,直线l1:y=kx+b与x轴交于点B(1,0),直线l2:$y=\frac{1}{2}x+1$与y轴交于点C,这两条直线交于点A(2,a).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC在平面直角坐标系中.
如图,△ABC在平面直角坐标系中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com