Question

【题目】已知正方形ABCD，点E，F分别在射线AB，射线BC上，AE=BF，DE与AF交于点O.

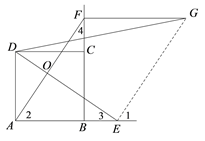
（1）如图1，当点E，F分别在线段AB，BC上时，则线段DE与AF的数量关系是 ，位置关系是 .

（2）如图2，当点E在线段AB延长线上时，将线段AE沿AF进行平移至FG，连接DG.

①依题意将图2补全；

②小亮通过观察、实验提出猜想：在点E运动的过程中，始终有.

小亮把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

想法1：连接EG，要证明，只需证四边形FAEG是平行四边形及△DGE是等腰直角三角形.

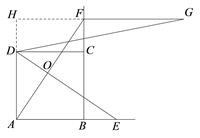
想法2：延长AD，GF交于点H，要证明，只需证△DGH是直角三角形.

图1 图2

请你参考上面的想法，帮助小亮证明.（一种方法即可）

Answer 1

【答案】（1）相等，垂直；（2）①补图见解析；②证明见解析

【解析】解：（1）相等，垂直．.

（2）①依题意补全图形．.

②法1：

证明：连接GE.

由平移可得AE=FG，AE∥FG，∴四边形AEGF是平行四边形.

∴AF=EG，AF∥EG，

∴∠1=∠2.

∵四边形ABCD是正方形，

∴AD = AB，∠DAE=∠ABC= 90°.

∵AE=BF，

∴△AED≌△BFA.

∴∠3=∠4，AF = DE.

∴EG=DE.

∵∠2+∠4=90°，

∴∠1+∠3=90°，∴∠DEG=90°.

∴.

又 ∵，

∴.

法2：

证明：延长AD，GF交于点H，

由平移可得AE=FG，AE∥FG，

∴∠H+∠DAB= 180°

∵四边形ABCD是正方形，

∴∠DAB= 90°，AD=DC.

∴∠H = 90°.

∴.

∵∠HDC=∠DCF= 90°,

∴四边形HDCF是矩形.

∴HF=DC.

∴HF=AD.

∵HG=FG+HF,

∴HG=AE+HF=AE+AD.

∵易证BF=AH 且BF=AE,

∴HD=AE –AD.

∴.