
已知:△ABC内接于圆O,OA是半径,AD⊥BC于D点,
求证:∠BAO=∠DAC.
|
证法一:过 O点作OF⊥AB于E,交圆O于F点,如图所示
∵ O为圆心,∴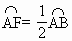
∴∠ C的度数等于 的度数 的度数
∴∠ O=∠C∵ AD⊥BC于D,∴∠ AEO=∠ADC=90°∴∠ BAO=∠DAC证法二:如图所示,延长 AO交圆O于E点,
连接 BE则∠ BEA=∠C∵ AO是⊙O的半径∴ AE为⊙O的直径∴∠ EBA=90°∴∠ BAO+∠BEA=90°在△ ABC中,AD⊥BC于D∴∠ C+∠DAC=90°又∵∠ C=∠BEA∴∠ BAO=∠DAC证法三:如图所示,延长 AO交圆O于E,连接CE
∵ AE是直径,∴∠ACE=90°∵ AD⊥BC,∴∠ADB=90°∴∠ ADB=∠ACE∵∠ B=∠E,∴∠BAD=∠EAC∵∠ DAC=∠EAC-∠EAD,且∠ BAO=∠BAD-∠EAD∴∠ BAO=∠DAC证法四:如图所示,分别延长 AO、AD交圆O于E、F点,连接EF
∵ AE是直径∴∠ F=90°又AD⊥BC∵∠ ADB=90°∴ EF∥BC∴ ∴∠ BAE=∠CAF即∠BAO=∠DAC四种不同的证法从不同的角度利用了圆周角定理及其推论,证法二和证法三还用到了垂径定理及其推论.这体现了运用知识的灵活性.另外,证题中一些常用辅助线的作法,如作出弦的弦心距,构造直径所对的圆周角等要认真体会. |


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
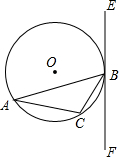 已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且∠CBF=∠A.
已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且∠CBF=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•南开区一模)如图,已知:△ABC内接于⊙O,点D在OC的延长线上,∠B=∠D=30°.
(2013•南开区一模)如图,已知:△ABC内接于⊙O,点D在OC的延长线上,∠B=∠D=30°.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com