
【题目】如图,△ABC中,∠BAC=90°,AB=AC,在△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
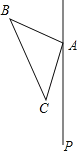
(1)依题意补全图形;
(2)若∠PAC=24°,求∠AEB的度数;
(3)连结CE,若AE=![]() ,CE=1,求BE长.
,CE=1,求BE长.
【答案】(1)图形如图所示:见解析;(2)∠AEB=45°;(3)BE=3.
【解析】
(1)根据要求作出对称点,连线画出图形即可;
(2)根据图形的对称性,得出△ACD和△ADB是等腰三角形,利用∠AEB=∠EAD+∠ADE,求出∠EAD,∠ADE.
(3)在BE上截取BF=ED,连接AF,证明△ABF≌△ADE(SAS),得出BE=DF,利用勾股定理,求出EF即得.
(1)作直线AP,作点C的对称点D,连接AD,BD,图形如图所示:
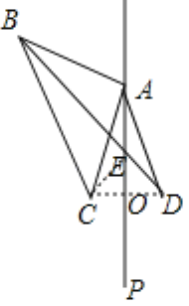
(2)∵C,D关于PA对称,
∴∠PAC=∠PAD=24°,
∴∠CAD=48°,
∵∠BAC=90°,
∴∠BAD=90°+48°=138°,
∴∠ADB=∠ABD=![]() (180°-138°)=21°,
(180°-138°)=21°,
∴∠AEB=∠EAD+∠ADE=21°+24°=45°.
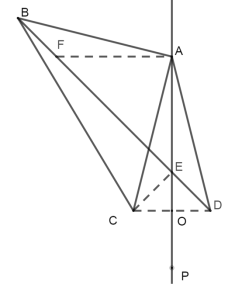
(3)如图,在BE上截取BF=ED,连接AF,由(1)中作图可知,
AC=AD,CE=DE,
又∵AB=AC,
∴AB=AD,则![]()
在△ABF和△ADE中

∴△ABF≌△ADE(SAS),
∴AF=AE,∠BAF=∠DAE=∠CAE,
∴∠FAE=∠FAC+∠CAE=∠FAC+∠BAC=∠BAC=90°,
∴EF=![]() AE=2,
AE=2,
又BF=ED=CE=1,
∴BE=BF+EF=1+2=3.
故答案为:3.


科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,
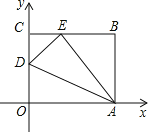
(1)求D、E两点的坐标.
(2)求过D、E两点的直线函数表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子AC长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.4米到A′,那么梯子的底端在水平方向滑动了几米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
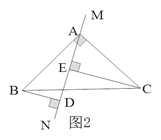
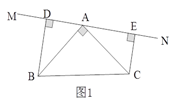
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O 相离,OA⊥l于点A,交⊙O 于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=2![]() ,OA=3,求线段PB的长.
,OA=3,求线段PB的长.
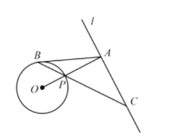
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com