
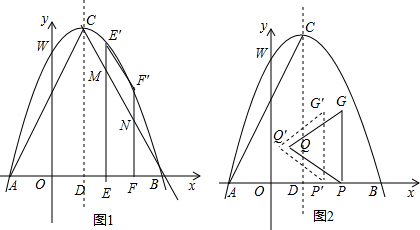
分析 (1)求出抛物线与x轴的交点坐标和顶点坐标,用待定系数法求解析式即可;
(2)先求出E′、F′的坐标表示,然后求出E′M、F′N,用二次函数的顶点坐标求出当m=3时,ME′+NF′的值最大,得到E′、F′的坐标,再求出E′F′的解析式,当点R在直线E′F′与y轴的交点时,|RF′-RE′|的最大值,从而求出R点的坐标及|RF′-RE′|的最大值;
(3)分类讨论Q点在∠WAB的角平分线或外角平分线上时,运用三角形相似求出相应线段,在求出△Q′P′G′与△ADC的重叠部分面积为S.
解答 解:(1)令y=0,则-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+3$\sqrt{3}$=0,
解方程得:x=6或x=-2,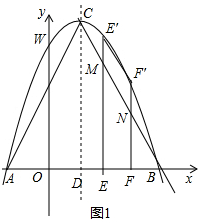
∴A(-2,0),B(6,0),
又y=-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+3$\sqrt{3}$=-$\frac{\sqrt{3}}{4}$(x-2)2+4$\sqrt{3}$,
又顶点C(2,4$\sqrt{3}$),
设直线BC的解析式为:y=kx+b,代入B、C两点坐标得:
$\left\{\begin{array}{l}{6k+b=0}\\{2k+b=4\sqrt{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=6\sqrt{3}}\end{array}\right.$,
∴y=-$\sqrt{3}$x+6$\sqrt{3}$;
(2)如图1,
∵点E(m,0),F(m+2,0),
∴E′(m,-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+3$\sqrt{3}$),F′(m+2,-$\frac{\sqrt{3}}{4}$m2+4$\sqrt{3}$),
∴E′M=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+3$\sqrt{3}$-(-$\sqrt{3}$m+6$\sqrt{3}$)=-$\frac{\sqrt{3}}{4}$m2+2$\sqrt{3}$m-3$\sqrt{3}$,
F′N=-$\frac{\sqrt{3}}{4}$m2+4$\sqrt{3}$-(-$\sqrt{3}$m+4$\sqrt{3}$)=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m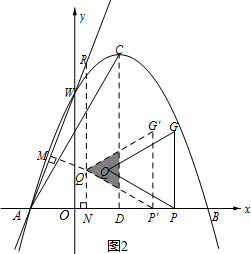 ,
,
∴E′M+F′N=-$\frac{\sqrt{3}}{4}$m2+2$\sqrt{3}$m-3$\sqrt{3}$+(-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m)=-$\frac{\sqrt{3}}{2}$m2+3$\sqrt{3}$m-3$\sqrt{3}$,
当m=-$\frac{3\sqrt{3}}{2×(-\frac{\sqrt{3}}{2})}$=3时,E′M+F′N的值最大,
∴此时,E′(3,$\frac{15\sqrt{3}}{4}$)F′(5,$\frac{7\sqrt{3}}{4}$),
∴直线E′F′的解析式为:y=-$\sqrt{3}$x+$\frac{27\sqrt{3}}{4}$,
∴R(0,$\frac{27\sqrt{3}}{4}$),
根据勾股定理可得:RF′=10,RE′=6,
∴|RF′-RE′|的值最大值是4;
(3)由题意得,Q点在∠WAB的角平分线或外角平分线上,
①如图2,当Q点在∠WAB的角平分线上时,
Q′M=Q′N=$\sqrt{3}$,AW=$\sqrt{31}$,
∵△RMQ′∽△WOA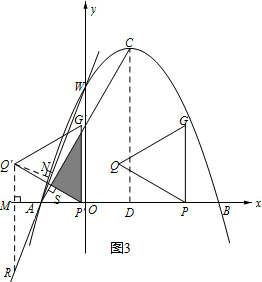 ,
,
∴$\frac{RQ′}{WA}=\frac{MQ′}{AO}$
∴RQ′=$\frac{\sqrt{93}}{2}$,
∴RN=$\frac{\sqrt{93}}{2}$+$\sqrt{3}$,
∵△ARN∽△AWO,
∵$\frac{AO}{AN}=\frac{WO}{RN}$
∴AN=$\frac{2+\sqrt{31}}{3}$,
∴DN=AD-AN=4-$\frac{2+\sqrt{31}}{3}$=$\frac{10-\sqrt{31}}{3}$,
∴S=$\frac{131\sqrt{3}-20\sqrt{93}}{27}$;
②如图3,当Q点在∠WAB的外角平分线上时,
∵△Q′RN∽△WAO,
∴RQ′=$\frac{\sqrt{93}}{2}$,
∴RM=$\frac{\sqrt{93}}{2}$-$\sqrt{3}$,
∵△RAM∽△WOA,
∴AM=$\frac{\sqrt{31}-2}{3}$,
在RtQ′MP′中,MP′=$\sqrt{3}$Q′M=3,
∴AP′=MP′-AM=3-$\frac{\sqrt{31}-2}{3}$=$\frac{11-\sqrt{31}}{3}$,
在Rt△AP′S中,P′S=$\frac{\sqrt{3}}{2}$AP′=$\frac{\sqrt{3}}{2}$×$\frac{11-\sqrt{31}}{3}$,
∴S=$\frac{76\sqrt{3}-11\sqrt{93}}{12}$.
点评 本题主要考查了待定系数法求函数解析式,二次函数的性质,三角形的三边关系,三角形相似的判定与性质以及数形结合和分类讨论思想的综合运用,此题牵扯知识面广,综合性强,难度较大.


科目:初中数学 来源: 题型:选择题
| A. | x≥-2且x≠0 | B. | x>-2 且x≠0 | C. | x>0 | D. | x≤-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
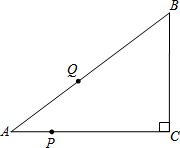 如图,已知Rt△ABC中,∠C=90°,AC=8,BC=6,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都停止运动,设点P,Q运动的时间为t秒.
如图,已知Rt△ABC中,∠C=90°,AC=8,BC=6,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都停止运动,设点P,Q运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3x2y-x2y=3 | C. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | D. | (a2b)3=a6b3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com