
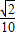 ,问:
,问: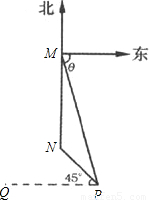
 .MN=70
.MN=70 -10
-10 =60
=60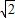 ,PN=10
,PN=10 =20.根据路程,速度,时间的关系即可求解.
=20.根据路程,速度,时间的关系即可求解.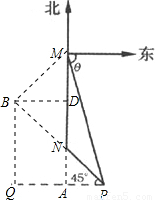 解:(1)延长MN交PQ于点A.
解:(1)延长MN交PQ于点A.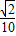 =10
=10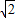 ,
, =
= =70
=70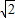 .
.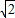 .
.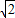 -10
-10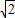 =60
=60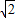 .
.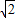 AN=10
AN=10 =20.
=20.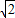 .
. t.
t.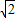 t-10
t-10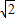 ,MD=AM-BQ=70
,MD=AM-BQ=70 -10
-10 t.
t.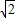 t-10
t-10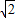 )2+(70
)2+(70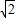 -10
-10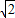 t)2=(20+10t)2.
t)2=(20+10t)2.

科目:初中数学 来源: 题型:
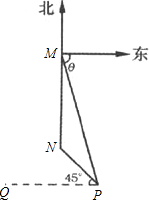 域,当前半径为20千米,并以10千米/小时的速度不断增大,已知cosθ=
域,当前半径为20千米,并以10千米/小时的速度不断增大,已知cosθ=
| ||
| 10 |
查看答案和解析>>
科目:初中数学 来源:第31章《锐角三角函数》中考题集(42):31.3 锐角三角函数的应用(解析版) 题型:解答题
 ,问:
,问: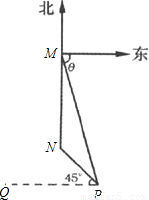
查看答案和解析>>
科目:初中数学 来源:第4章《锐角三角形》中考题集(39):4.3 解直角三角形及其应用(解析版) 题型:解答题
 ,问:
,问:
查看答案和解析>>
科目:初中数学 来源:2006年山东省烟台市中考数学试卷(课标卷)(解析版) 题型:解答题
 ,问:
,问: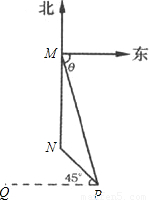
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com