
分析 如图,C(a,b),利用矩形的性质和反比例函数图象上点的坐标特征分别表示出A(a,0),E(a,$\frac{k}{a}$),B(0,b),F($\frac{k}{b}$,b),利用三角形面积公式得到S△ECF=$\frac{1}{2}$(b-$\frac{k}{a}$)(a-$\frac{k}{b}$),S△OEF=ab-k-S△ECF,于是得到S=S△OEF-S△ECF=k-$\frac{{k}^{2}}{ab}$,接着利用S=-$\frac{{k}^{2}}{12}$+k可解得ab=12,然后利用2≤a≤4得到2≤$\frac{12}{b}$≤4,然后解关于b的不等式组即可.
解答 解:如图,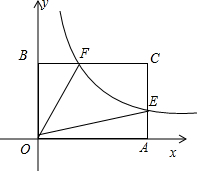 C(a,b),则A(a,0),E(a,$\frac{k}{a}$),B(0,b),F($\frac{k}{b}$,b),
C(a,b),则A(a,0),E(a,$\frac{k}{a}$),B(0,b),F($\frac{k}{b}$,b),
∵S△ECF=$\frac{1}{2}$(b-$\frac{k}{a}$)(a-$\frac{k}{b}$),S△OEF=ab-$\frac{1}{2}$k-$\frac{1}{2}$k-S△ECF=ab-k-S△ECF=
∴S=S△OEF-S△ECF=ab-k-2S△ECF
=ab-k-ab+k+k-$\frac{{k}^{2}}{ab}$
=k-$\frac{{k}^{2}}{ab}$,
而S=-$\frac{{k}^{2}}{12}$+k,
∴-$\frac{{k}^{2}}{12}$+k=k-$\frac{{k}^{2}}{ab}$,
∴ab=12,
即a=$\frac{12}{b}$,
∵2≤a≤4,
∴2≤$\frac{12}{b}$≤4,
∴3≤b≤6.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数图象上点的坐标特征和三角形面积公式.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
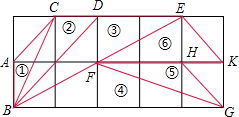 如图,在正方形网格上有6个斜三角形:
如图,在正方形网格上有6个斜三角形:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
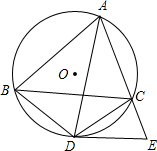 如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.
如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
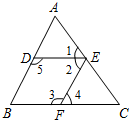 推理填空:如图,根据图形填空
推理填空:如图,根据图形填空查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).
如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8011.5×108 | B. | 801.15×109 | C. | 8.0115×1010 | D. | 8.0115×1011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com