
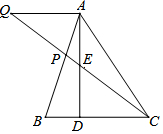
 在△ABC中,AD是高,E是AD的中点,连接CE并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
在△ABC中,AD是高,E是AD的中点,连接CE并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.分析 (1)设BD=x,根据题意用x表示出CD、AD、BC,根据相似三角形的性质列出比例式,计算即可;
(2)根据勾股定理求出CE,根据三角形中位线定理求出CQ,根据相似三角形的性质列式计算即可.
解答 解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴$\frac{AQ}{CD}$=$\frac{AE}{DE}$=1,
∴AQ=CD=2x,
∴$\frac{AP}{PB}$=$\frac{AQ}{BC}$=$\frac{2}{3}$;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=$\frac{1}{2}$AD=7.5,
由勾股定理得,CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\frac{25}{2}$,
∴CQ=25,
∵AQ∥BC,
∴$\frac{QP}{PC}$=$\frac{AQ}{BC}$=$\frac{2}{3}$,
∴CP=10.
点评 本题相似三角形的判定和性质、三角形中位线定理,掌握相似三角形的判定定理和性质定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x-6=0 | B. | 3(x-2)-2(x-3)=5x | C. | $\frac{3x+3}{2}$=6 | D. | $\frac{x-1}{4}$=$\frac{3-2x}{6}$-$\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
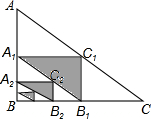 如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
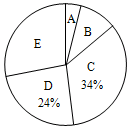 某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.
某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.| 组别 | 分数段(x) | 频数 |
| A | 0≤x<60 | 2 |
| B | 60≤x<70 | 5 |
| C | 70≤x<80 | 17 |
| D | 80≤x<90 | a |
| E | 90≤x≤100 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com