
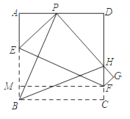
【题目】如图,现有一张边长为![]() 的正方形ABCD,点P 为正方形 AD 边上的一点(不与点 A、点D 重合),将正方形纸片折叠,使点 B 落在 P 处,点 C 落在 G 处,PG 交DC 于H,折痕为 EF,连接 BP,BH.
的正方形ABCD,点P 为正方形 AD 边上的一点(不与点 A、点D 重合),将正方形纸片折叠,使点 B 落在 P 处,点 C 落在 G 处,PG 交DC 于H,折痕为 EF,连接 BP,BH.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当点P在边AD上移动时,△PDH的周长是否发生变化?不变化,求出周长,若变化,说明理由;
(4)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式.
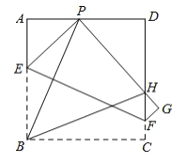
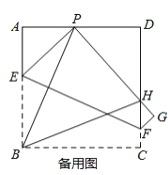
【答案】(1)见解析(2)见解析(3)周长固定,周长为![]() .(4)
.(4)![]()
【解析】
(1)根据折叠的性质,对应边相等,即能解决问题.(2)根据折叠的性质和问题(1)的结论即能解决问题.(3)通过证明过B点向PG作垂线,垂足为Q,通过分别证明 ![]() 和
和![]() ,将△PDH的周长问题转化成两固定边长之和,即能解决问题,
,将△PDH的周长问题转化成两固定边长之和,即能解决问题,
(1)证明:∵四边形EPGF由四边形EFCB折叠而来,EB与EP重叠
∴EP = EB
∴∠EPB = ∠EBP
(2)证明∵四边形EPGF由四边形EFCB折叠而来,EB与EP重叠,PG与BC重叠
∴∠EPG = ∠EBC
又∵∠EPB = ∠EBP
∴∠EPG - ∠EPB = ∠EBC - ∠EBP,即
∠BPH = ∠PBC
∵ AD∥BC,
∴∠APB = ∠PBC,
∴∠APB = ∠BPH
(3)解:△PDH的周长不发生变化.
如图所示,过点B作BQ丄PG于点Q.
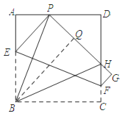
在△BPA和△BPQ中,
∵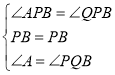 ,
,
∴![]()
∴ ![]()
∴![]()
![]()
![]()
![]() ,
,
∵![]()
∴ ![]()
∴QH=HC
∴△PDH的周长为:![]()
为固定值,固定不变.
如图,过点F作FM垂直AB于点M.
∵![]()
∴![]()
在△ABP和△MFE中
∵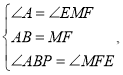
∴![]()
∴ ![]()
在△AEP中,根据勾股定理,可得:
![]()
解得:![]()
∴![]() ,即
,即

即S关于x的关系式为:
![]()


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.

(1)求证:AE=CF;
(2)求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() 将
将![]() 绕点
绕点![]() .按顺时针方向旋转
.按顺时针方向旋转![]() 得
得![]() , 连接
, 连接![]() .
.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时, 试判断
时, 试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
(1)求桥DC与直线AB的距离;
(2)现在从A地到达B地可比原来少走多少路程?
(以上两问中的结果均精确到0.1km,参考数据:![]() ≈1.14,
≈1.14,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的高,D是AM上的点,以CD为一边,在CD的下方作等边△CDE,连结BE.
(1)填空:∠ACB=____;∠CAM=____;
(2)求证:△AOC≌△BEC;
(3)延长BE交射线AM于点F,请把图形补充完整,并求∠BFM的度数;
(4)当动点D在射线AM上,且在BC下方时,设直线BE与直线AM的交点为F.∠BFM的大小是否发生变化?若不变,请在备用图中面出图形,井直接写出∠BFM的度数;若变化,请写出变化规律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与x轴和y轴分别交于点A和B,再将
的图像与x轴和y轴分别交于点A和B,再将![]() 沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
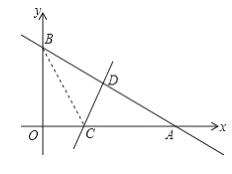
(1)求点A和点B的坐标;
(2)求![]() ;
;
(3)在y轴上有一点P,且![]() 是等腰三角形,求出点P的坐标.
是等腰三角形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
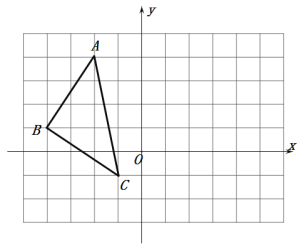
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,4),B(-4,1),C(-1,-1)
(1)直接写出△ABC的面积;
(2)在图中作出△ABC关于x轴的对称△A1B1C1;
(3)将△ABC向右平移5个单位,向上平移一个单位,得到△A2B2C2,并写出B2的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com