
【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB= ![]() .
.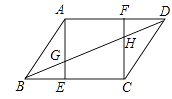
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴∠CDF=∠ABE,DC=AB= ![]() ,
,
∵tan∠ABE=2,
∴tan∠CDF=2,∵CF⊥AD,
∴△CFD是直角三角形,
∴ ![]() =2,设DF=x,则CF=2x,
=2,设DF=x,则CF=2x,
在Rt△CFD中,由勾股定理可得(2x)2+x2=( ![]() )2,
)2,
解得x=2或x=﹣2(舍去),
∴CF=4;
(2)解:证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵AE⊥BC,CF⊥AD,∴AE⊥AD,CF⊥BC,
∴∠GAD=∠HCB=90°,
∴△AGD≌△CHB,
∴BH=DG,
∴BG=DH.
【解析】(1)由平行四边形的性质,结合三角函数的定义,在Rt△CFD中,可求得CF=2DF,再利用勾股定理可求得CF的长。
(2)利用平行四边形的性质结合条件可证得△AGD≌△CHB,则可求得BH=DG,从而可证得BG=DH。


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
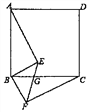
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
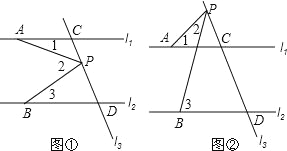
【题目】已知直线 l1∥l2,l3 和 l1,l2 分别交于 C,D 两点,点 A,B 分别在线 l1,l2 上,且位于 l3 的左 侧,点 P 在直线 l3 上,且不和点 C,D 重合.
(1)如图 1,有一动点 P 在线段 CD 之间运动时,试确定∠1、∠2、∠3 之间的关系,并给出证明;
(2)如图 2,当动点 P 在线段 CD 之外运动时,上述的结论是否成立?若不成立,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数 ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 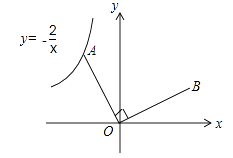
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的一点,
边上的一点,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着边
出发,以每秒1个单位的速度沿着边![]() 向终点
向终点![]() 运动,连接
运动,连接![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.

(1)求![]() 的长;
的长;
(2)当![]() 为多少秒时,
为多少秒时,![]() 是直角三角形?
是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
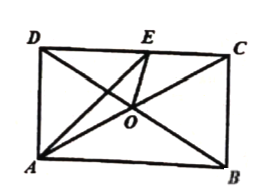
【题目】如图,在矩形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,给出以下结论:①
,给出以下结论:①![]() 为等腰直角三角形;②
为等腰直角三角形;②![]() 为等边三角形;③
为等边三角形;③![]() ;④
;④![]() ⑤
⑤![]() 是
是![]() 的中位线.其中正确的结论有( )
的中位线.其中正确的结论有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
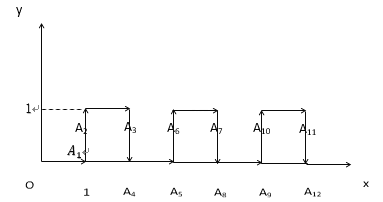
【题目】在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1个单位长度,其行走的路线如图所示,第1次移动到A1,第2次移动到A2……,第n次移动到An,则三角形OA2A2018的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com