
【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.

【答案】(1)220;110;(2)∠E+∠F=180°.理由见解析;(3)AB∥CD.
【解析】试题分析:(1)先根据三角形内角和定理求出∠FBC+∠BCF=180°-∠F=110°,再由角平分线定义得出∠ABC=2∠FBC,∠BCD=2∠BCF,那么∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=220°;由四边形ABCD的内角和为360°,得出∠BAD+∠CDA=360°-(∠ABC+∠BCD)=140°.由角平分线定义得出∠DAE=![]() ∠BAD,∠ADE=
∠BAD,∠ADE=![]() ∠CDA,那么∠DAE+∠ADE=
∠CDA,那么∠DAE+∠ADE=![]() ∠BAD+
∠BAD+![]() ∠CDA=
∠CDA=![]() (∠BAD+∠CDA)=70°,然后根据三角形内角和定理求出∠E=180°-(∠DAE+∠ADE)=110°;
(∠BAD+∠CDA)=70°,然后根据三角形内角和定理求出∠E=180°-(∠DAE+∠ADE)=110°;
(2)由四边形ABCD的内角和为360°得到∠BAD+∠CDA+∠ABC+∠BCD=360°,由角平分线定义得出∠DAE+∠ADE+∠FBC+∠BCF=180°,又根据三角形内角和定理有∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,那么∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,于是∠E+∠F=360°-(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)由(2)可知∠E+∠F=180°,如果∠E=∠F,那么可以求出∠E=∠F=90°,根据三角形内角和定理求出∠DAE+∠ADE=90°,再利用角平分线定义得到∠BAD+∠CDA=180°,于是AB∥CD.
试题解析:(1)∵∠F=70,
∴FBC+∠BCF=180°∠F=110°.
∵∠ABC、∠BCD的角平分线交于点F,
∴∠ABC=2∠FBC,∠BCD=2∠BCF,
∴∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=220°;
∵四边形ABCD的内角和为360°,
∴∠BAD+∠CDA=360°(∠ABC+∠BCD)=140°.
∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,
∴∠DAE=![]() ∠BAD,∠ADE=
∠BAD,∠ADE=![]() ∠CDA,
∠CDA,
∴∠DAE+∠ADE=![]() ∠BAD+
∠BAD+![]() ∠CDA=
∠CDA=![]() (∠BAD+∠CDA)=70°,
(∠BAD+∠CDA)=70°,
∴∠E=180°(∠DAE+∠ADE)=110°;
故答案为:220;110;
(2)∠E+∠F=180°.理由如下:
∵∠BAD+∠CDA+∠ABC+∠BCD=360°,
∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F,
∴∠DAE+∠ADE+∠FBC+∠BCF=180°,
∵∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,
∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,
∴∠E+∠F=360°-(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)AB∥CD.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 、
、![]() 、
、![]() 三点的坐标分别为
三点的坐标分别为![]() 、
、![]() 、
、![]() .
.

(1)画出![]() ,则
,则![]() 的面积为_______;
的面积为_______;
(2)在![]() 中,点
中,点![]() 经过平移后的对应点为
经过平移后的对应点为![]() ,将
,将![]() 作同样的平移得到
作同样的平移得到![]() ,画出平移后的
,画出平移后的![]() ,并写出点
,并写出点![]() ,
,![]() 的坐标
的坐标![]() (_______);
(_______);![]() (_______);
(_______);
(3)![]() 为
为![]() 中一点,将点
中一点,将点![]() 向右平移4个单位,再向下平移6个单位得到点
向右平移4个单位,再向下平移6个单位得到点![]() ,则
,则![]() _______,
_______,![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm. 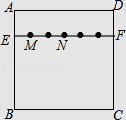
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.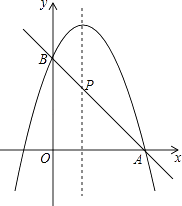
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.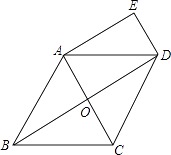
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.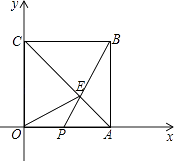
(1)求点E的坐标:
(2)求△OPE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com