
【题目】如图,点![]() 在
在![]() 上,点
上,点![]() 是
是![]() 外一点.
外一点.![]() 切
切![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
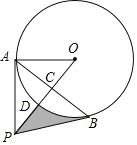
【答案】(1)见解析;(2)18![]() ﹣6π
﹣6π
【解析】
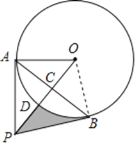
(1)连接OB,由垂径定理得OP垂直平分AB,进而证明△APO≌△BPO,得∠PAO=∠PBO,结合PA切⊙O于点A, 即可得到结论;
(2)先证△APB是等边三角形,设OB=x,则OP=2x,由勾股定理得OB=6,结合三角形的面积公式和扇形的面积公式,即可求解.
(1)连接OB,
∵OP⊥AB,OP经过圆心O,
∴AC=BC,
∴OP垂直平分AB,
∴AP=BP,
∵OA=OB,OP=OP,
∴△APO≌△BPO(SSS),
∴∠PAO=∠PBO,
∵PA切⊙O于点A,
∴AP⊥OA,
∴∠PAO=90°,
∴∠PBO=∠PAO=90°,
∴OB⊥BP,
又∵点B在⊙O上,
∴PB是⊙O的切线;
(2)∵PA切⊙O于点A, PB切⊙O于点B,
∴PA=PB,
∵∠APB=60°,
∴△APB是等边三角形,
∴PB=AB=6![]() ,
,
在Rt△OPB中,
∵∠OPB=∠OPA=![]() ∠APB=30°,
∠APB=30°,
∴OP=2OB,∠POB=60°,
设OB=x,则OP=2x,
由勾股定理得: x2+(6![]() )2=(2x)2
)2=(2x)2
∵x>0
∴x=6 , 即OB=6,
∴S△OPB=![]() ×BP×OB=
×BP×OB=![]() ×6
×6![]() ×6=18
×6=18![]() ,S扇DOB=
,S扇DOB=![]() =6π,
=6π,
∴S阴影=S△OPB﹣S扇DOB=18![]() ﹣6π.
﹣6π.


科目:初中数学 来源: 题型:
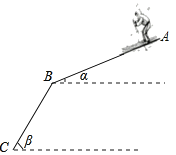
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润![]() (单位:元)与售价
(单位:元)与售价![]() (单位:元/千克)之间的函数关系式.
(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
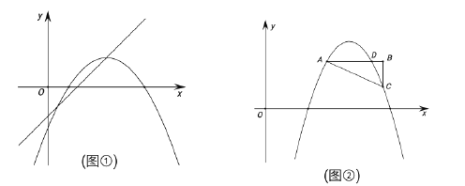
【题目】如图①,将抛物线![]() 平移到顶点恰好落在直线
平移到顶点恰好落在直线![]() 上,并设此时抛物线顶点的横坐标为
上,并设此时抛物线顶点的横坐标为![]() .
.
(1)求抛物线的解析式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)如图②,![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() ,
,![]() 轴,
轴,![]() ,
,![]() .
.
①求![]() 的面积(用含
的面积(用含![]() 的代数式表示);
的代数式表示);
②若![]() 的面积为1,当
的面积为1,当![]() 时,
时,![]() 的最大值为-3,求
的最大值为-3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+4x+5.
(1)用配方法将y=-x2+4x+5化成y=a(x﹣h)2+k的形式;
(2)指出抛物线的开口方向、对称轴和顶点坐标;
(3)若抛物线上有两点A(x1,y1),B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是AB边的中点,点E为AC中点,点F在边BC上,AF交DE于点G,点H是FC的中点,连接GH.

(1)如图1,求证:四边形GHCE是平行四边形;
(2)如图2,当AB=AC,点F是BC中点时,在不添加任何辅助线的情况下,请直接写出图中所有长度等于![]() BF的线段.
BF的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是

A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一组方程:①![]() ,②
,②![]() ,③
,③![]() ,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为
,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为![]() ;第②个方程的解为
;第②个方程的解为![]() ;第③个方程的解为
;第③个方程的解为![]() .若n为正整数,且关于x的方程
.若n为正整数,且关于x的方程![]() 的一个解是
的一个解是![]() ,则n的值等于____________.
,则n的值等于____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com