
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD.
(1)求该抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,若经过点P的直线PE与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出直线PE的解析式;若不存在,请说明理由.
解:(1)由题意得:OC=4,OD=2,∴DM=OC+OD=6。
∴顶点M坐标为(2,6)。
设抛物线解析式为:y=a(x﹣2)2+6,
∵点C(0,4)在抛物线上,∴4=4a+6,解得a=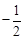 。
。
∴抛物线的解析式为:y=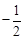 (x﹣2)2+6=
(x﹣2)2+6=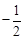 x2+2x+4。
x2+2x+4。
(2)如答图1,过点P作PE⊥x轴于点E.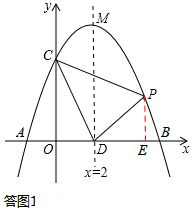
∵P(x,y),且点P在第一象限,∴PE=y,OE=x。
∴DE=OE﹣OD=x﹣2.
∴S=S梯形PEOC﹣S△COD﹣S△PDE= (4+y)•x﹣
(4+y)•x﹣ ×2×4﹣
×2×4﹣ (x﹣2)•y=y+2x﹣4。
(x﹣2)•y=y+2x﹣4。
将y=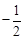 x2+2x+4代入上式得:S=
x2+2x+4代入上式得:S=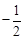 x2+2x+4+2x﹣4=
x2+2x+4+2x﹣4=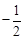 x2+4x。
x2+4x。
在抛物线解析式y=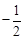 x2+2x+4中,令y=0,即
x2+2x+4中,令y=0,即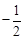 x2+2x+4=0,解得x=2±
x2+2x+4=0,解得x=2±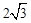 .
.
设抛物线与x轴交于点A、B,则B(2+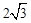 ,0)。
,0)。
∴0<x<2+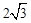 .
.
∴S关于x的函数关系式为:S=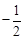 x2+4x(0<x<2+
x2+4x(0<x<2+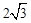 )。
)。
(3)存在。若以O、P、E为顶点的三角形与△OPD全等,可能有以下情形:
①OD=OP。
由图象可知,OP最小值为4,即OP≠OD,故此种情形不存在。
②OD=OE。
若点E在y轴正半轴上,如答图2所示,此时△OPD≌△OPE。
∴∠OPD=∠OPE,即点P在第一象限的角平分线上。
∴直线PE的解析式为:y=x。
若点E在y轴负半轴上,易知此种情形下,两个三角形不可能全等,故不存在。
③OD=PE。
∵OD=2,∴第一象限内对称轴右侧的点到y轴的距离均大于2。
∴点P只能位于对称轴左侧或与顶点M重合。
若点P位于第一象限内抛物线对称轴的左侧,易知△OPE为钝角三角形,而△OPD为锐角三角形,则不可能全等。
若点P与点M重合,如答图3所示,此时△OPD≌OPE,四边形PDOE为矩形。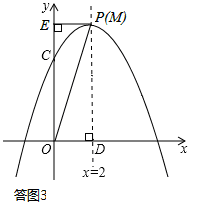
∴直线PE的解析式为:y=6。
综上所述,存在以O、P、E为顶点的三角形与△OPD全等,直线PE的解析式为y=x或y=6。
解析试题分析:(1)首先求出点M的坐标,然后利用顶点式和待定系数法求出抛物线的解析式。
(2)如答图1所示,作辅助线构造梯形,利用S=S梯形PEOC﹣S△COD﹣S△PDE求出S关于x的表达式;求出抛物线与x轴正半轴的交点坐标,得到自变量的取值范围。
(3)由于三角形的各边,只有OD=2是确定长度的,因此可以以OD为基准进行分类讨论:
①OD=OP,因为第一象限内点P到原点的距离均大于4,因此OP≠OD,此种情形排除。
②OD=OE.分析可知,只有如答图2所示的情形成立。
③OD=PE.分析可知,只有如答图3所示的情形成立。


科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;
(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | |
| 销售玩具获得利润w(元) | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.
(1)求菱形ABCD的周长;
(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;
(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,抛物线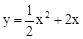 与x轴相交于O、B,顶点为A,连接OA.
与x轴相交于O、B,顶点为A,连接OA.
(1)求点A的坐标和∠AOB的度数;
(2)若将抛物线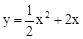 向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
(3)在(2)的情况下,判断点C′是否在抛物线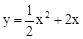 上,请说明理由;
上,请说明理由;
(4)若点P为x轴上的一个动点,试探究在抛物线m上是否存在点Q,使以点O、P、C、Q为顶点的四边形是平行四边形,且OC为该四边形的一条边?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2 与x轴交于点A(﹣1,0)、B(4,0).点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
(1)求这条抛物线所对应的函数关系式.
(2)求点C在这条抛物线上时m的值.
(3)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.
①当点D在这条抛物线的对称轴上时,求点D的坐标.
②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时,直接写出所有符合条件的m值.
(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,平面直角坐标系中,以点C(2, )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
2011年11月28日至12月9日,联合国气候变化框架公约第17次缔约方会议在南非德班召开,大会通过了“德班一揽子决议”(DurbanPackageOutcome),建立德班增强行动平台特设工作组,决定实施《京都议定书》第二承诺期并启动绿色气候基金,中国的积极态度赢得与会各国的尊重.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活逐渐成为人们的共识.某企业采用技术革新,节能减排.从去年1至6月,该企业二氧化碳排放量y1(吨)与月份x(1≤x≤6,且x取整数)之间的函数关系如下表:
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| 二氧化碳排放量y1(吨) | 600 | 300 | 200 | 150 | 120 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
点(﹣1,y1),(2,y2),(3,y3)均在函数y= 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )
| A.y3<y2<y1 | B.y2<y3<y1 |
| C.y1<y2<y3 | D.y1<y3<y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com