
【题目】如图1,抛物线y=ax2-3ax-2交x轴于A、B(A左B右)两点,交y轴于点C,过C作CD∥x轴,交抛物线于点D,E(-2,3)在抛物线上.
(1)求抛物线的解析式;
(2)P为第一象限抛物线上一点,过点P作PF⊥CD,垂足为F,连接PE交y轴于G,求证:FG∥DE;
(3)如图2,在(2)的条件下,过点F作FM⊥PE于M.若∠OFM=45°,求P点坐标.

【答案】(1)y=![]() x2-
x2-![]() x-2;(2)见解析;(3)点P坐标为(6,7)
x-2;(2)见解析;(3)点P坐标为(6,7)
【解析】
(1)把点E坐标代入抛物线解析式即求得a的值;
(2)由抛物线解析式求点A、B、C、D的坐标,直接求得直线DE解析式为y=-x+1.设点P横坐标为t,即得到点F(t,-2).把t当常数用待定系数法求直线PE解析式,进而求得用t表示的点G纵坐标,再用待定系数法求直线FG解析式,解得FG解析式的一次项系数为-1,与直线DE相等,所以FG∥DE;
(3)延长FO、PE相交于点N,由FM⊥PE于M且∠OFM=45°可证得△MNF为等腰直角三角形,故有FM=MN.过点M作MG⊥PF于点G,过点N作NH⊥PM于点H,即构造出△FGM≌△MHN,进而有FG=MH,MG=NH.设点M横坐标为m,由(2)求得的直线PE解析式可得M的纵坐标,进而得到用t和m表示的MG、FG.求直线OF解析式,联立直线OF与直线PE求得用t表示的交点N坐标,进而得到用t和m表示的MH、NH.代入FG=MH,MG=NH即得到关于t、m的二元方程组,解方程组并考虑t的范围即求得点P坐标.
解:(1)∵E(-2,3)在抛物线y=ax2-3ax-2上
∴4a+6a-2=3
解得:a=![]()
∴抛物线解析式为y=![]() x2-
x2-![]() x-2
x-2
(2)证明:∵y=![]() x2-
x2-![]() x-2=0时,解得:x1=-1,x2=4
x-2=0时,解得:x1=-1,x2=4
∴A(-1,0),B(4,0)
∵x=0时,y=![]() x2-
x2-![]() x-2=-2
x-2=-2
∴C(0,-2)
∵点D在抛物线上,且CD∥x轴
∴D(3,-2)
设直线DE解析式为y=kx+b
∴![]() 解得:
解得:![]()
∴直线DE:y=-x+1
∵点P为第一象限抛物线上一点
∴设点P坐标为(t,![]() t2-
t2-![]() t-2)(t>4)
t-2)(t>4)
设直线PE解析式为y=cx+d
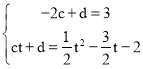 解得:
解得: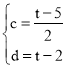
∴直线PE:y=![]() x+t-2,直线PE与y轴交点G(0,t-2)
x+t-2,直线PE与y轴交点G(0,t-2)
∵PF⊥CD于点F
∴F(t,-2)
设直线FG解析式为y=ex+t-2
把点F代入得:te+t-2=-2
解得:e=-1
∴FG∥DE
(3)延长FO、PE相交于点N,过点M作MG⊥PF于点G,过点N作NH⊥PM于点H

∴∠FGM=∠MHN=90°
∵FM⊥PE于M
∴∠FMN=90°
∴∠FMG+∠NMH=∠MNH+∠NMH=90°
∴∠FMG=∠MNH
∵∠OFM=45°
∴∠MNF=180°-∠FMN-∠OFM=45°
∴FM=MN
在△FGM与△MHN中
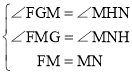
∴△FGM≌△MHN(AAS)
∴FG=MH,MG=NH
∵F(t,-2)
∴直线OF:y=-![]() x
x
∵点M在直线PE:y=![]() x+t-2上
x+t-2上
∴设M(m,![]() m+t-2)
m+t-2)
∴MG=t-m,FG=![]() m+t-2-(-2)=
m+t-2-(-2)=![]() m+t
m+t
∵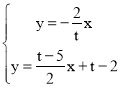 解得:
解得: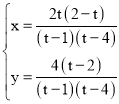
∴N(![]() ,
,![]() )
)
∴MH=m-![]() ,NH=
,NH=![]() m+t-2-
m+t-2-![]()
∴
解得: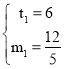
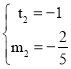 (舍去)
(舍去)
∴yP=![]() ×36-
×36-![]() ×6-2=7
×6-2=7
∴点P坐标为(6,7).


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生,为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》,某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量。该饲养场2019年每月生猪产量y(吨)与月份x(![]() ,且x为整数)之间的函数关系如图所示.
,且x为整数)之间的函数关系如图所示.
(1)请直接写出当![]() (x为整数)和
(x为整数)和![]() (x为整数)时,y与x的函数关系式;
(x为整数)时,y与x的函数关系式;
(2)若该饲养场生猪利润P(万元/吨)与月份x(![]() ,且x为整数)满足关系式:
,且x为整数)满足关系式:![]() ,请问:该饲养场哪个月的利润最大?最大利润是多少?
,请问:该饲养场哪个月的利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校七年级4个班共180人的体质健康情况,从各班分别抽取同样数量的男生和女生组成一个样本,如图是根据样本绘制的条形图和扇形图.

(1)本次抽查的样本容量是______.
(2)请补全条形图和扇形图中的百分数;
(3)请你估计全校七年级共有多少人优秀.
查看答案和解析>>
科目:初中数学 来源: 题型:
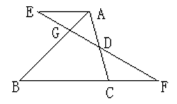
【题目】已知:点D是△ABC中AC的中点,AE∥BC,ED交AB于点G,交BC的延长线于点F.
(1)求证:△GAE∽△GBF;
(2)求证:AE=CF;
(3)若BG:GA=3:1,BC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
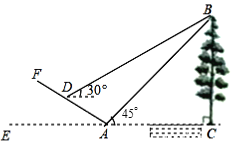
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
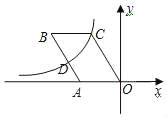
A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com