
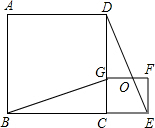
 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列4个结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列4个结论:分析 由四边形ABCD和四边形CEFG是正方形,根据正方形的性质,即可得BC=DC,CG=CE,∠BCD=∠ECG=90°,则可根据SAS证得①△BCG≌△DCE;然后延长BG交DE于点H,根据全等三角形的对应角相等,求得∠CDE+∠DGH=90°,则可得②BH⊥DE;由△DGO与△DCE相似即可判定③错误,证明△EFO∽△DGO,即可求得④正确;即可得出结论.
解答 解:①∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,CD∥EF,
∴∠BCG=∠DCE.
在△BCG和△DCE中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCG=∠DCE}&{\;}\\{CG=CE}&{\;}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
故①正确;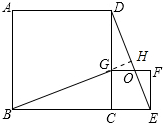
②延长BG交DE于点H,如图所示:
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
又∵∠CBG+∠BGC=90°,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BH⊥DE;
∴BG⊥DE.
故②正确;
③∵四边形GCEF是正方形,
∴GF∥CE,
∴$\frac{DG}{DC}=\frac{GO}{CE}$,
∴$\frac{DG}{GC}=\frac{GO}{CE}$错误,③错误;
④∵DC∥EF,
∴△DGO∽△EOF,
∴$\frac{{S}_{△DGO}}{{S}_{△EOF}}$=($\frac{a-b}{b}$)2=$\frac{(a-b)^{2}}{{b}^{2}}$,
∴$\frac{{S}_{△EOF}}{{S}_{△DGO}}$=($\frac{EF}{DG}$)2=($\frac{b}{a-b}$)2=$\frac{{b}^{2}}{(a-b)^{2}}$,④正确;
正确的有①②④;
故答案为:①②④.
点评 本题主要考查正方形的性质、全等三角形的判定和性质及相似三角形的判定和性质,综合性较强,掌握三角形全等、相似的判定和性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,试判断四边形AECF是什么样的四边形?写出你的结论并予以证明.
如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,试判断四边形AECF是什么样的四边形?写出你的结论并予以证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 旋转一定会改变图形的形状和大小 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| D. | 相等的角是对顶角 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com