
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
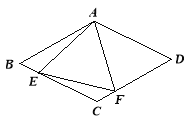
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
【答案】(1)证明过程见解析;(2)4+2![]()
【解析】
试题分析:(1)连接AC,根据菱形的性质以及∠BAD=120°得出∠BAE=∠FAC以及△ABC和△ACD为正三角形,从而得出△ABE和△ACF全等,从而得出答案;(2)根据三角形全等得出△ABE的面积=△ACF的面积,从而得出四边形AECF的面积=△ABC的面积,从而求出△ABC的面积得出四边形的面积,根据垂线段最短得出当正三角形AEF的边AE与BC垂直时,边AE最短,从而求出最小值.
试题解析:(1)如图,连接AC∵四边形ABCD为菱形,∠BAD=120°,
∠BAE+∠EAC=60°,∠FAC+∠EAC=60°,∴∠BAE=∠FAC
∵∠BAD=120°,∴∠ABC=60°.∴△ABC和△ACD为等边三角形
∴∠ACF=60°,AC=AB ∴∠ABE=∠AFC ∴在△ABE和△ACF中,∵∠BAE=∠FAC,AB=AC,∠ABE=∠AFC,∴△ABE≌△ACF(ASA) ∴BE=CF
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,则![]() .∴
.∴![]() ,是定值
,是定值
作AH⊥BC于H点,则BH=2,
![]() .
.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4+![]() ,
,




 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0),B(2,0),与y轴相交于点C.
(1)求二次函数的解析式;
(2)若点E是第一象限的抛物线上的一个动点,当四边形ABEC的面积最大时,求点E的坐标,并求出四边形ABEC的最大面积;
(3)若点M在抛物线上,且在y轴的右侧.⊙M与y轴相切,切点为D.以C,D,M为顶点的三角形与△AOC相似,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)求二月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型每台进价为3500元,乙型每台进价为4000元,预计用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)对于(2)中刚进货的20台两种型号的手机,该店计划对甲型号手机在二月份售价基础上每售出一台甲型手机再返还顾客现金a元,乙型手机按销售价4400元销售,若要使(2)中所有方案获利相同,a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
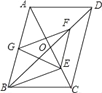
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有![]() 、
、![]() 、
、![]() 三地,甲、乙两车同时从
三地,甲、乙两车同时从![]() 地出发,分别匀速前柱
地出发,分别匀速前柱![]() 地、
地、![]() 地,甲车到达
地,甲车到达![]() 地停留一段时间后原速原路返回,乙车到达
地停留一段时间后原速原路返回,乙车到达![]() 地后立即原速原路返回(掉头时间忽略不计),乙车比甲车早1小时返回
地后立即原速原路返回(掉头时间忽略不计),乙车比甲车早1小时返回![]() 地,甲、乙两车各自行驶的路程
地,甲、乙两车各自行驶的路程![]() (千米)与时间
(千米)与时间![]() (时)(从两车出发时开始计时)之间的变化情况如图所示.
(时)(从两车出发时开始计时)之间的变化情况如图所示.

(1)在这个变化过程中,自变量是______,因变量是______.
(2)甲车到达![]() 地停留的时长为______小时,乙车从出发到返回
地停留的时长为______小时,乙车从出发到返回![]() 地共用了______小时.
地共用了______小时.
(3)甲车的速度是______千米/时,乙车的速度是______千米/时.
(4)![]() 、
、![]() 两地相距______千米,甲车返回
两地相距______千米,甲车返回![]() 地途中
地途中![]() 与
与![]() 之间的关系式是______(不必写出自变量取值范围).
之间的关系式是______(不必写出自变量取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
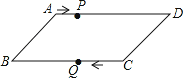
A. 4次 B. 3次 C. 2次 D. 1次
查看答案和解析>>
科目:初中数学 来源: 题型:
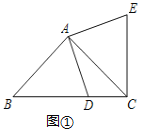
【题目】基本图形:在RT△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.
探索:(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明结论;
(2)连接DE,如图②,试探索线段DE,BD,CD之间满足的等量关系,并证明结论;
联想:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=7,CD=2,则AD的长为 .
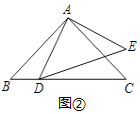
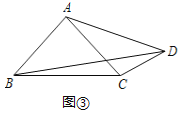
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=12cm,动点P从点A出发以1cm/s的速度沿AC匀速运动,动点Q同时从点B出发以同样的速度沿CB的延长线方向匀速运动,当点P到达点C时,点P,Q同时停止运动.设运动时间为ts,过点P作PE⊥AB于点E,连接PQ交AB于点D.
⑴当t为何值时,△CPQ为直角三角形?
⑵求DE的长.
⑶取线段BC的中点M,连接PM,将△CPM沿直线PM翻折,得到△C,PM,连接AC,,当t= 时,AC,的值最小,最小值为 .
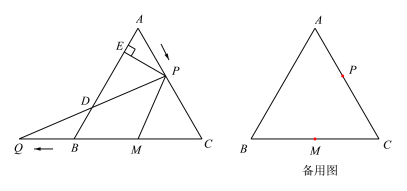
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com