
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的弧经过点
为半径的弧经过点![]() 是弧
是弧![]() 上一个动点.
上一个动点.
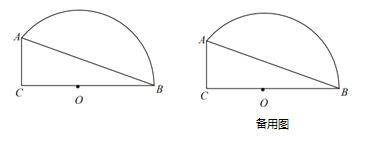
![]() 求半径
求半径![]() 的长;
的长;
![]() 如果点
如果点![]() 是弧
是弧![]() 的中点,联结
的中点,联结![]() ,求
,求![]() 的正切值;
的正切值;
![]() 如果
如果![]() 平分
平分![]() ,延长
,延长![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)9;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理得到AB=![]() =12
=12![]() ,如图1,过O作OH⊥AB于H,根据相似三角形的性质即可得到结论;
,如图1,过O作OH⊥AB于H,根据相似三角形的性质即可得到结论;
(2)如图2,连接OP交AB于H,根据垂径定理得到OP⊥AB,AH=BH=![]() AB=6
AB=6![]() ,得到PH=9-3=6,根据圆周角定理得到∠PCB=∠PBA,根据三角函数的定义即可得到结论;
,得到PH=9-3=6,根据圆周角定理得到∠PCB=∠PBA,根据三角函数的定义即可得到结论;
(3)如图3,过A作AE⊥BD于E,连接CP,根据角平分线的性质得到AE=AC=4![]() ,根据相似三角形的性质得到AD=
,根据相似三角形的性质得到AD=![]() ,根据全等三角形的性质得到BE=BC=16,根据勾股定理和三角形的面积公式即可得到结论.
,根据全等三角形的性质得到BE=BC=16,根据勾股定理和三角形的面积公式即可得到结论.
解:![]() )∵Rt△ABC中,∠ACB=90°,AC=4
)∵Rt△ABC中,∠ACB=90°,AC=4![]() ,BC=16,
,BC=16,
∴AB=![]() =12
=12![]() ,
,
如图1,过O作OH⊥AB于H,
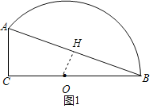
则BH=![]() AB=6
AB=6![]() ,
,
∵∠BHO=∠ACB=90°,∠B=∠B,
∴△BHO∽△BCA,
∴![]()
∴![]()
∴OB=9;
(2) 如图2,连接OP交AB于H,连结![]() ,交
,交![]() 于点
于点![]() ,
,
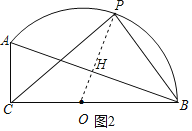
![]() 是弧
是弧![]() 的中点,
的中点,![]() 过圆心
过圆心
![]() , AH=BH=
, AH=BH=![]() AB=6
AB=6![]() ,
,
在Rt△BHO中,OH=![]() =
=![]() =3,
=3,
∴PH=9-3=6,
∵点P是弧AB的中点,
∴弧AP=弧PB,
∴∠PCB=∠PBA,
∴∠PCB的正切值=∠PBA的正切值=![]() =
=![]() ;
;
![]() 如图3,过A作AE⊥BD于E,连接CP,
如图3,过A作AE⊥BD于E,连接CP,
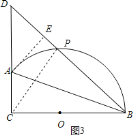
∵BA平分∠PBC,AC⊥BC,
∴AE=AC=4![]() ,
,
∵∠AED=∠ACB=90°,∠D=∠D,
∴△ADE∽△BDC,
∴![]() ,
,
设DE=x,
∴![]() ,
,
∴AD=![]()
在Rt△ACB与Rt△AEB中,![]()
∴Rt△ACB≌Rt△AEB(HL),
∴BE=BC=16,
∵CD2+BC2=BD2,
∴(4![]() +
+![]() )2+162=(16+x)2,
)2+162=(16+x)2,
解得:x=![]()
∴AD=![]() ,BD=16+
,BD=16+![]() =
=![]() ,
,
∴CD=![]()
∵BC是⊙的直径,
∴CP⊥BD,
∴CP=![]() =
=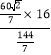 =
= ![]()
∴PD=![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
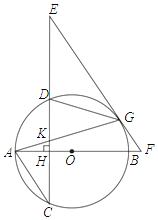
查看答案和解析>>
科目:初中数学 来源: 题型:
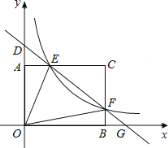
【题目】如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B.C重合),过点F的反比例函数y=![]() 的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为
的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为![]() ;②若k=
;②若k=![]() ,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=
,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=![]() ,则k=1.其中正确的命题的序号是____________(填序号).
,则k=1.其中正确的命题的序号是____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了安全,交通部门一再提醒司机:请勿超速!同时,进一步完善各类监测系统,如图,在松铜公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了测速点C,从测速点C测得一小车从点A到达点B行驶了3秒钟,已知∠CAN=45°,∠CBN=60°,BC=120米.
(1)求测速点C到该段公路的距离;
(2)请你通过计算判断此车是否超速,(结果精确到0.1m/s)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
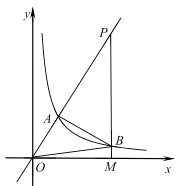
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条直线与反比例函数![]() 的图像交于
的图像交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点,![]() 轴,垂足为
轴,垂足为![]() .
.
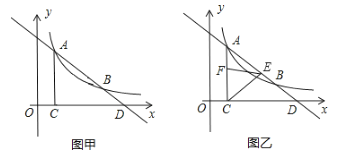
(1)如图甲,求反比例函数的解析式与![]() 点的坐标;
点的坐标;
(2)如图乙,若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,作
,作![]() ,
,![]() 交
交![]() 于
于![]() 点.试说明
点.试说明![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建设工地一个工程有大量的沙石需要运输.建设公司车队有载重量为8吨和10吨的卡车共12辆,全部车辆一次能运输110吨沙石
(1)求建设公司车队载重量为8吨和10吨的卡车各有多少辆?
(2)随着工程的进展,车队需要一次运输沙石超过160吨,为了完成任务,准备新增购这两种卡车共6辆,车队最多新购买载重量为8吨的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为![]() 元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于
元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数
(元/件)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)写出销售单价![]() 的取值范围;
的取值范围;
(2)求出一次函数![]() 的解析式;
的解析式;
(3)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
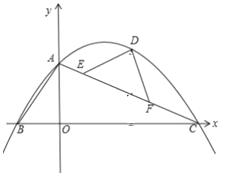
【题目】如图,平面直角坐标系中,O为坐标原点,直线y=﹣![]() x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=
x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=![]() .
.
(1)求抛物线的解析式;
(2)已知E、F是线段AC上异于A、C的两个点,且AE<AF,EF=2![]() ,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
(3)在(2)的条件下,当∠EDF=90°时,连接BD,P为抛物线上一动点,过P作PQ⊥BD交线段BD于点Q,连接EQ.设点P的横坐标为t,求t为何值时,PE=QE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com