
【题目】问题提出



(1)如图1,![]() 的边BC在直线n上,过顶点A作直线m∥n,在直线m上任取一点D连接BD,CD,则
的边BC在直线n上,过顶点A作直线m∥n,在直线m上任取一点D连接BD,CD,则![]() 的面积_______
的面积_______![]() 的面积(填“等于”大于”或“小于”)
的面积(填“等于”大于”或“小于”)
问题探究
(2)如图2,在菱形ABCD和菱形BGFE中,![]() ,求
,求![]() 的面积.
的面积.
问题解决
(3)如图3在矩形ABCD中,![]() ,在矩形ABCD内(可以在边上)存在点P,使得
,在矩形ABCD内(可以在边上)存在点P,使得![]() 的面积等于矩形ABCD的面积的
的面积等于矩形ABCD的面积的![]() ,求
,求![]() 周长的最小值.
周长的最小值.
【答案】(1)等于;(2)![]() 的面积是
的面积是![]() ;(3)
;(3)![]() 周长的最小值是32.
周长的最小值是32.
【解析】
(1)两条平行线间的距离一定,那么△ABC与△ABD同底等高,所以面积相等;
(2)连接BD,根据已知条件和菱形的性质可得![]() ,由(1)可得
,由(1)可得![]() ,
,
求出等边三角形BGE即可得出答案;
(3)过点P作![]() ,交DA于点F,交BC于点G,作点B关于FG的对称点B',连接
,交DA于点F,交BC于点G,作点B关于FG的对称点B',连接![]() ,根据两点之间线段最短得出
,根据两点之间线段最短得出![]() 从而得出
从而得出![]() ,再根据
,再根据![]() 的面积等于矩形ABCD的面积的
的面积等于矩形ABCD的面积的![]() ,得出BG的长,
,得出BG的长,
继而求出![]() 的长,即可得出答案;
的长,即可得出答案;
(1)∵m∥n,
∴![]() 和
和![]() 同底等高;
同底等高;
∴![]() 的面积=
的面积=![]() 的面积
的面积
故答案为:等于;
(2)如图1,连接BD,过点B作![]() 于点H.
于点H.
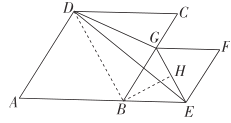
∴四边形ABCD和四边形BEFG是菱形,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
![]()
![]()
在![]() 中,
中,![]() ,
,
![]()
![]() 的面积是
的面积是![]()
(3)如图2,过点P作![]() ,交DA于点F,交BC于点G,作点B关于FG的对称点B',连接
,交DA于点F,交BC于点G,作点B关于FG的对称点B',连接![]() .
.
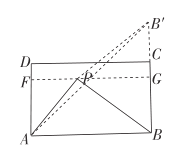
![]() 的面积是矩形ABCD的面积的
的面积是矩形ABCD的面积的![]() ,
,
∴P是FG上的一动点
∵点B与B’关于FG对称,
![]()
![]() ,
,
即![]()
![]()
![]() 的面积是矩形ABCD的面积的
的面积是矩形ABCD的面积的![]() ,
,
![]() 边AB边上的高是8,
边AB边上的高是8,
![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
综上,![]() 周长的最小值是32.
周长的最小值是32.


科目:初中数学 来源: 题型:
【题目】如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
(1)问:“姐妹两人同时选中同一根绳子”这一事件是 事件,概率是 ;
(2)在互相看不见的条件下,姐姐先将左侧A、C两个绳端打成一个连结,则妹妹从右侧A1、B1、C1三个绳端中随机选两个打一个结(打结后仍能自由地通过木孔);请求出“姐姐抽动绳端B,能抽出由三根绳子连结成一根长绳”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD是平行四边形,两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?
(2)求出此时菱形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在![]() 轴上.
轴上.
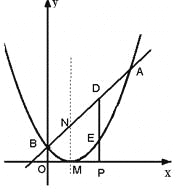
(1)求m的值及这个二次函数的解析式;
(2)若P(![]() ,0) 是
,0) 是![]() 轴上的一个动点,过P作
轴上的一个动点,过P作![]() 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<![]() < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要用篱笆(虚线部分)成一个矩形苗圃![]() ,其中两边靠的墙足够长,中间用平行于
,其中两边靠的墙足够长,中间用平行于![]() 的篱笆
的篱笆![]() 隔开,已知篱笆的总长度为18米,设矩形苗圃
隔开,已知篱笆的总长度为18米,设矩形苗圃![]() 的一边
的一边![]() 的长为
的长为![]() ,矩形苗圃
,矩形苗圃![]() 面积为
面积为![]() .
.

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求所围矩形苗圃![]() 的面积最大值;
的面积最大值;
(3)当所围矩形苗圃![]() 的面积为
的面积为![]() 时,则
时,则![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
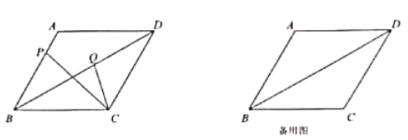
【题目】已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设![]() ,求y关于
,求y关于![]() 的函数解析式及定义域;
的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果![]() 与
与![]() 相似,求线段BP的长.
相似,求线段BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com