
分析 (1)运用古典概率,有六种相等可能的结果,出现鲜肉馅粽子有两种结果,根据概率公式,即可求解;
(2)此题可以认为有两步完成,所以可以采用树状图法或者采用列表法;注意题目属于不放回实验,利用列表法即可求解.
解答 解:(1)她吃到肉馅的概率是$\frac{2}{1+2+3}$=$\frac{1}{3}$;
故答案为:$\frac{1}{3}$;
(2)如图所示:根据树状图可得,一共有30种等可能的情况,吃两个粽子,一个枣馅、一个肉馅只有12种情况,所以她吃到一个枣馅、一个肉馅的概率=$\frac{12}{30}$=$\frac{2}{5}$.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,注意是否是放回还是不放回事件是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
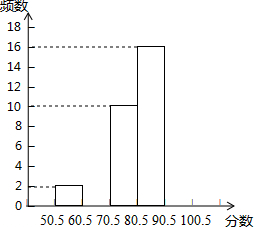 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)| 分组 | 频数 | 频率 |
| 50.5~60.5 | 2 | 0.04 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | C |
| A~90.5 | B | 0.32 |
| 90.5~100.5 | 14 | 0.28 |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
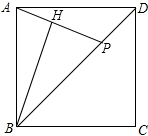 已知正方形ABCD的边长是2,点P从点D出发沿DB向点B运动,至点B停止运动,连结AP,过点B作BH⊥AP于点H,在点P运动过程中,点H所走过的路径长是π.
已知正方形ABCD的边长是2,点P从点D出发沿DB向点B运动,至点B停止运动,连结AP,过点B作BH⊥AP于点H,在点P运动过程中,点H所走过的路径长是π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=4 | B. | x=5 | C. | x=6 | D. | x=7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com