
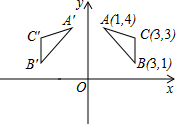
 如图,△A′B′C′与△ABC关于y轴对称,已知A(1,4),B(3,1),C(3,3),若以原点O为位似中心,相似比为$\frac{1}{2}$作△A′B′C′的缩小的位似图形△A″B″C″,则A″的坐标是(-$\frac{1}{2}$,2)或($\frac{1}{2}$,-2).
如图,△A′B′C′与△ABC关于y轴对称,已知A(1,4),B(3,1),C(3,3),若以原点O为位似中心,相似比为$\frac{1}{2}$作△A′B′C′的缩小的位似图形△A″B″C″,则A″的坐标是(-$\frac{1}{2}$,2)或($\frac{1}{2}$,-2). 分析 先根据△A′B′C′与△ABC关于y轴对称,A(1,4),即可得出A'(-1,4),再根据以原点O为位似中心,相似比为$\frac{1}{2}$作△A′B′C′的缩小的位似图形△A″B″C″,可得A″的坐标.
解答  解:如图所示,∵△A′B′C′与△ABC关于y轴对称,A(1,4),
解:如图所示,∵△A′B′C′与△ABC关于y轴对称,A(1,4),
∴A'(-1,4),
∵相似比为$\frac{1}{2}$,
∴A“(-$\frac{1}{2}$,2)或($\frac{1}{2}$,-2).
故答案为:(-$\frac{1}{2}$,2)或($\frac{1}{2}$,-2).
点评 本题主要考查了位似变换以及轴对称变换的运用,解题时注意::①画一个图形的位似图形时,位似中心的选择是任意的,这个点可以在图形的内部或外部或在图形上,对于具体问题要考虑画图方便且符合要求.②由于位似中心选择的任意性,因此作已知图形的位似图形的结果是不唯一的.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com