
【题目】如图,在△ABC中,∠ACB=![]() ,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2) 当∠A=![]() 时,求证:四边形ECBF是菱形.
时,求证:四边形ECBF是菱形.

【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据三角形的中位线定理可得EF∥BC,根据两组对边分别平行的四边形是平行四边形即可判定四边形ECBF是平行四边形;(2)根据直角三角形中30°的锐角所对的直角边等于斜边的一半和斜边的中线等于斜边的一半可得![]() ,
, ![]() ,即可得
,即可得![]() ,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
试题解析: (1) 证明:∵D,E分别为边AC,AB的中点,
∴DE∥BC,即EF∥BC.
又∵BF∥CE,
∴四边形ECBF是平行四边形.
(2)证法一:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,
, ![]() .
.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法二:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,∠ABC=
,∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法三:
∵E为AB的中点,∠ACB=![]() ,∠A=
,∠A=![]() ,
,
∴![]() , ∠ABC=
, ∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.


科目:初中数学 来源: 题型:
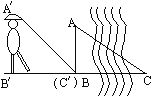
【题目】如图所示,传说在19世纪初,一位将军率领部队在一河边与敌军激战,为使炮弹准确地落在河对岸的敌军阵地,将军站在河这岸,将帽檐压低,使视线沿着帽檐恰好落在河对岸的边线上,然后他向后退(保证B′、B、C在一条直线上),一直退到视线落在河这岸的边线上为止,这时,他后退的距离就等于河宽,这是为什么?请给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 要了解一批灯泡的使用寿命应采用普方式
B. “任意画出一个等边三角形,它是轴对称图形”是随机事件
C. 有一组数据:3,5,7,6,4,这组数据的中位数是5.
D. 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(1)求点A、B、D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)在x>0的条件下,根据图象说出反比例函数的值大于一次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会关注.“寒假”期间,记者小刘随机调查了某区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:
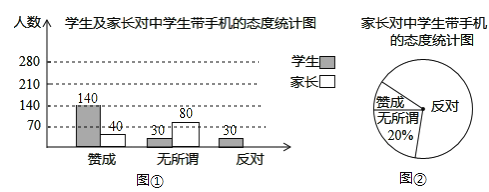
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)若该区共有中学生8000人,请根据以上图表信息估算出该区中学生中对“校园手机”持“无所谓”态度的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com