

分析 根据三角形面积公式,长方形面积公式,正方形面积公式即可求出答案.
解答 解:(1)S△AGD=$\frac{1}{2}$(a+b)(2a-b)=a2+$\frac{1}{2}$ab-$\frac{1}{2}$b2;
(2)S阴影=(a+b)b-$\frac{1}{2}$(a+b)(2a-b)-$\frac{1}{2}$a2
=2b2-$\frac{3}{2}$a2+$\frac{1}{2}$ab
(3)当a=30,b=50时,
S阴影=2×502-$\frac{3}{2}$×302+$\frac{1}{2}$×50×30=4400(m2)
故答案为:(1)a2+$\frac{1}{2}$ab-$\frac{1}{2}$b2;
点评 本题考查列代数式,涉及整式混合运算,以及代入求值问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
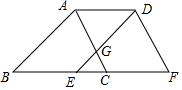 如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为4.
如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
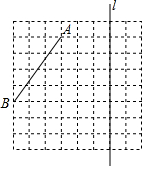 如图,在8×8的正方形网格纸中每个小正方形的边长都是1,线段AB的端点在小正方形的顶点上,直线l经过网格线.
如图,在8×8的正方形网格纸中每个小正方形的边长都是1,线段AB的端点在小正方形的顶点上,直线l经过网格线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
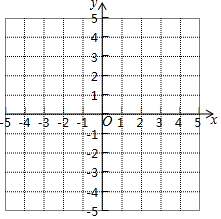 已知二次函数y=x2-2x.
已知二次函数y=x2-2x.| x | … | … | |||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 +y2,那么被墨汁遮住的一项应是( )
+y2,那么被墨汁遮住的一项应是( )| A. | -7xy | B. | -xy | C. | 7xy | D. | +xy |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com