
【题目】在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y![]() 与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
(1)求点B的坐标;
(2)当点P的横坐标为2时,求k的值;
(3)连接PO,记△POB的面积为S.若![]() ,结合函数图象,直接写出k的取值范围.
,结合函数图象,直接写出k的取值范围.
【答案】(1)点B的坐标为(0,2);(2)k的值为8;(3)![]() k<3.
k<3.
【解析】
(1)有点A的坐标,可求出直线的解析式,再由解析式求出B点坐标.
(2)把点P的横坐标代入直线解析式即可求得点P的纵坐标,然后把点P代入反比例函数解析式即可得k值.
(3)根据△POB的面积为S的取值范围求点P的横坐标取值,然后把横坐标代入直线解析式,即可求得点P纵坐标的取值范围,进而求得k的取值范围.
解:(1)∵直线l:y=x+b与x轴交于点A(﹣2,0)
∴﹣2+b=0
∴b=2
∴一次函数解析式为:y=x+2
∴直线l与y轴交于点B为(0,2)
∴点B的坐标为(0,2);
(2)∵双曲线y![]() 与直线l交于P,Q两点
与直线l交于P,Q两点
∴点P在直线l上
∴当点P的横坐标为2时,y=2+2=4
∴点P的坐标为(2,4)
∴k=2×4=8
∴k的值为8
(3)如图:
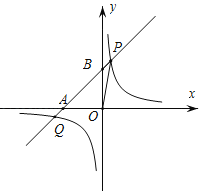
S△BOP![]() 2×xp=xp,
2×xp=xp,
∵![]() ,
,
∴![]() xp<1,
xp<1,
∴![]() yp<3,
yp<3,
∴![]() k<3
k<3


科目:初中数学 来源: 题型:
【题目】完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
小王同学参加某高中学校进行的自主招生考试,本次考试共有1000人参加.
(1)1000人参加自招考试,有300人可以享受加分政策,且有10,20,30,60四个档次,小王想获得至少30分的加分,那么概率为多少?
(2)若该高中的中考录取分数线为530分,小王估得中考分数可能在500-509,510-519,520-529三个分段,
①若小王的中考分数在510~519分段,则小王被该高中录取的概率为多少?
②若小王的中考分数在三个分数段对应的概率分别为![]() ,
,![]() ,
,![]() ,则小王被该高中录取的概率为多少?
,则小王被该高中录取的概率为多少?
加分 | 人数 |
10 | 30 |
20 | 90 |
30 | 150 |
60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
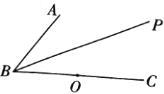
【题目】如图所示,在平面内,给定不在同一直线上的点![]() ,
,![]() ,
,![]() ,射线
,射线![]() 是
是![]() 的平分线,点
的平分线,点![]() 到点
到点![]() ,
,![]() ,
,![]() 的距离均等于
的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() ,图形
,图形![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,作
,作![]() 于点
于点![]() ,延长
,延长![]() 交图形
交图形![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求直线
,求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,
,![]() ,给出如下定义:若
,给出如下定义:若![]() ,
,![]() 为某个三角形的顶点,且边
为某个三角形的顶点,且边![]() 上的高
上的高![]() ,满足
,满足![]() ,则称该三角形为点
,则称该三角形为点![]() ,
,![]() 的“生成三角形”.
的“生成三角形”.
(1)已知点![]() ;
;
①若以线段![]() 为底的某等腰三角形恰好是点
为底的某等腰三角形恰好是点![]() ,
,![]() 的“生成三角形”,求该三角形的腰长;
的“生成三角形”,求该三角形的腰长;
②若![]() 是点
是点![]() ,
,![]() 的“生成三角形”,且点
的“生成三角形”,且点![]() 在
在![]() 轴上,点
轴上,点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的坐标为______;
的坐标为______;
(2)![]() 的圆心为点
的圆心为点![]() ,半径为2,点
,半径为2,点![]() 的坐标为
的坐标为![]() ,
,![]() 为直线
为直线![]() 上一点,若存在
上一点,若存在![]() ,是点
,是点![]() ,
,![]() 的“生成三角形”,且边
的“生成三角形”,且边![]() 与
与![]() 有公共点,直接写出点
有公共点,直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组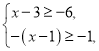
![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
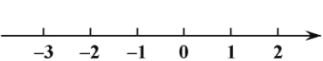
(Ⅳ)原不等式组的解集为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
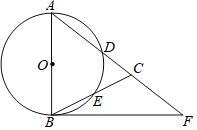
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠BAD=![]() ,求AD的长;
,求AD的长;
(3)试探究FB、FD、FA之间的关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com