
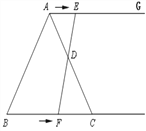
ЎҫМвДҝЎҝИзНјЈ¬ФЪөИұЯИэҪЗРОABCЦРЈ¬BC=6cm. ЙдПЯAG//BCЈ¬өгEҙУөгAіц·ўСШЙдПЯAGТФ1cm/sөДЛЩ¶ИФЛ¶ҜЈ¬Н¬КұөгFҙУөгBіц·ўСШЙдПЯBCТФ2cm/sөДЛЩ¶ИФЛ¶ҜЈ¬ЙиФЛ¶ҜКұјдОӘt(s) Ј»
ЈЁ1Ј©Б¬ҪУEFЈ¬өұEFҫӯ№эACұЯөДЦРөгDКұЈ¬ЗуЦӨЈәЎчADEЎХЎчCDFЈ»
(2)ЗуөұtОӘәОЦөКұЈ¬ЛДұЯРОACFEКЗБвРОЈ»
ЈЁ3Ј©КЗ·сҙжФЪДіТ»КұҝМtЈ¬К№ТФAЎўFЎўCЎўEОӘ¶ҘөгөДЛДұЯРОДЪҪЗіцПЦЦұҪЗЈҝИфҙжФЪЈ¬ЗуіцtөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ЦӨГчјыҪвОцЈ» (2)t=6Ј» ЈЁ3Ј©ҙжФЪЈ¬АнУЙјыҪвОцЈ®
ЎҫҪвОцЎҝ·ЦОцЈәЈЁ1Ј©УЙМвТвөГөҪAD=CDЈ¬ФЩУЙAGУлBCЖҪРРЈ¬АыУГБҪЦұПЯЖҪРРДЪҙнҪЗПаөИөГөҪБҪ¶ФҪЗПаөИЈ¬АыУГAASјҙҝЙөГЦӨЈ»ЈЁ2Ј©ИфЛДұЯРОACFEКЗБвРОЈ¬ФтУРCF=AC=AE=6Ј¬УЙEөДЛЩ¶ИЗуіцEФЛ¶ҜөДКұјдјҙҝЙЈ»ЈЁ3Ј©·ЦБҪЦЦЗйҝцҝјВЗЈәИфCEЎНAGЈ¬ҙЛКұЛДөг№№іЙИэҪЗРОЈ¬І»КЗЦұҪЗМЭРОЈ»ИфAFЎНBCЈ¬ЗуіцBFөДіӨ¶Иј°КұјдtөДЦөЈ®
ұҫМвҪвОцЈәЈЁ1Ј© ЦӨГчЈәЎЯAGЎОBC ,Ўа![]() ,ЎЯ
,ЎЯ![]() КЗACұЯөД,ЎаAD=CD
КЗACұЯөД,ЎаAD=CD
УЦЎЯ![]() , ЎаЎчADEЎХЎчCDF
, ЎаЎчADEЎХЎчCDF
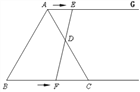
ЈЁ2Ј©ЎЯөұЛДұЯРОACFEКЗБвРОКұЈ¬ЎаAE=AC=CF=EF,
УЙМвТвҝЙЦӘЈәAE=t,CF=2T-6Ј¬Ўаt=6,
ЈЁ3Ј©өұЛДұЯРОДЪҪЗУРЦұҪЗКұЈ¬·ЦБҪЦЦЗйҝцЈәИфЛДұЯРОACFEКЗЦұҪЗМЭРОЈ¬ҙЛКұEFЎНAGЈ¬ №э![]() ЧчCMЎНAGУЪMЈ¬AM=3ҝЙТФөГөҪAE-CF=AMЈ¬
ЧчCMЎНAGУЪMЈ¬AM=3ҝЙТФөГөҪAE-CF=AMЈ¬
јҙt-(2t-6)=3,Ўаt=3Ј¬
ҙЛКұЈ¬CУлFЦШәПЈ¬І»·ыәПМвТвЈ¬ЙбИҘЎЈ
ИфЛДұЯРО![]() КЗЦұҪЗМЭРОЈ¬ҙЛКұAFЎНBCЈ¬
КЗЦұҪЗМЭРОЈ¬ҙЛКұAFЎНBCЈ¬
ЎЯЎчABCКЗөИұЯИэҪЗРОЈ¬FКЗBCЦРөгЈ¬
Ўа2t=3Ј¬ҫӯјмСйЈ¬·ыәПМвТвЈ¬Ўаt=![]() .
.


 ұҰұҙјЖ»®ЖЪД©іеҙМ¶б100·ЦПөБРҙр°ё
ұҰұҙјЖ»®ЖЪД©іеҙМ¶б100·ЦПөБРҙр°ё ДЬҝјКФИ«ДЬ100·ЦПөБРҙр°ё
ДЬҝјКФИ«ДЬ100·ЦПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ ПВБРЛө·ЁХэИ·өДКЗЈЁЎЎЎЎЈ©
A.¶ФҪЗПЯ»ҘПаҙ№ЦұөДЛДұЯРОКЗБвРОB.¶ФҪЗПЯПаөИөДЛДұЯРОКЗҫШРО
C.¶ФҪЗПЯПаөИөДМЭРОКЗөИСьМЭРОD.¶ФҪЗПЯПаөИЗТ»ҘПаЖҪ·ЦөДЛДұЯРОКЗХэ·ҪРО
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ1ДЙГЧ=10©Ғ9ГЧЈ¬ДіЦЦОўБЈөДЦұҫ¶ОӘ158ДЙГЧЈ¬УГҝЖС§јЗКэ·ЁұнКҫёГОўБЈөДЦұҫ¶ОӘГЧЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪОЪәЈЕﻧЗшёДФмЦРЈ¬УРТ»Іҝ·ЦВҘЕМТӘ¶ФНвПъКЫ. ДіВҘЕМ№І23ІгЈ¬ПъКЫјЫёсИзПВЈәөЪ°ЛІгВҘ·ҝКЫјЫОӘ4000ФӘЈҜГЧ2Ј¬ҙУөЪ°ЛІгЖрГҝЙПЙэТ»ІгЈ¬ГҝЖҪ·ҪГЧөДКЫјЫМбёЯ50ФӘЈ»·ҙЦ®Ј¬ҙУөЪ°ЛІгЖрГҝПВҪөТ»ІгЈ¬ГҝЖҪ·ҪГЧөДКЫјЫҪөөН30ФӘЈ¬ТСЦӘёГВҘЕМГҝМЧВҘ·ҝГж»эҫщОӘ120ГЧ2. Иф№әВтХЯТ»ҙОРФё¶ЗеЛщУР·ҝҝоЈ¬ҝӘ·ўЙМУРБҪЦЦУЕ»Э·Ҫ°ёЈә
·Ҫ°ёТ»ЈәҪөјЫ8%Ј¬БнНвГҝМЧВҘ·ҝФщЛНaФӘЧ°РЮ»щҪрЈ»
·Ҫ°ё¶юЈәЦ»ҪөјЫ10%Ј¬Г»УРЖдЛыФщЛН.
(1)ЗуіцКЫјЫyЈЁФӘЈҜГЧ2Ј©УлВҘІгxЈЁ1ЎЬxЎЬ23Ј¬xИЎХыКэЈ©Ц®јдөДәҜКэ№ШПөКҪЈ»
ЈЁ2Ј©ЦұҪУМоРҙҙр°ёЈәАПНхТӘ№әВтөЪК®БщІгөДТ»МЧВҘ·ҝЈ¬ЛыТ»ҙОРФё¶Зе№ә·ҝҝоЈ¬УГ·Ҫ°ёТ»Ј¬ХвМЧВҘ·ҝЧЬ·СУГОӘ__________ФӘЈ»өұa=__________КұБҪЦЦУЕ»Э·Ҫ°ёЧЬ·СУГПаН¬Ј»
өұa<__________КұЈ¬УГ·Ҫ°ё¶юәПЛг.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»ёцөИСьө«І»өИұЯөДИэҪЗРОЈ¬ЛьөДҪЗЖҪ·ЦПЯЈ¬ёЯЈ¬ЦРПЯөДЧЬМхКэОӘ_____МхЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИфЎчABCУлЎчDEFПаЛЖЈ¬ЖдГж»эұИОӘ4Јә9Ј¬ФтЎчABCУлЎчDEFөДПаЛЖұИОӘЈЁЎЎЎЎЈ©
A. 2Јә3B. 1Јә3C. 4Јә9D. 16Јә81
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝөұkЈҪ_____КұЈ¬¶аПоКҪx2+ЈЁk©Ғ1Ј©xy©Ғ3y2©Ғ2xy©Ғ5ЦРІ»ә¬xyПоЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЖҪ·ҪёщКЗЖдұҫЙнөДКэКЗ Ј¬Бў·ҪёщКЗЖдұҫЙнөДКэКЗ Ј¬ЖҪ·ҪКЗЖдұҫЙнөДКэКЗ Ј®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com