
分析 设共有x名员工去天华山旅游,根据每增加1人,人均旅游费用降低20元,且共支付给旅行社旅游费用27000元,可列出方程求解,根据人均旅游费用不得低于700元,判断解是否合理.
解答 解:∵25×1000=25000(元)<27000(元)
∴此次天华山旅游的人数超过25人.
设共有x名员工去天华山旅游,根据题意得:
x[1000-20(x-25)]=27000,
解这个方程得:x1=30,x2=45,
∵x=45时,1000-20×(45-25)=600<700,
∴x=45不符合题意,舍去.
∴只取x=30.
答:共有30名员工去天华山旅游.
点评 本题考查一元二次方程的应用,理解题意的能力,关键以支付给旅行社的费用作为等量关系列方程求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
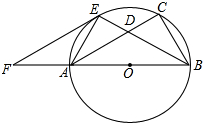 如图,已知以Rt△ABC的斜边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的斜边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
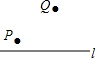 如图,直线1表示石家庄的太平河,点P表示朱河村,点Q表示黄庄村,欲在太平河1上修建一个水泵站(记为点M),分别向两村供水,现有如下四种修建水泵站供水管道的方案,图中实线表示修建的管道,则修建的管道最短的方案是( )
如图,直线1表示石家庄的太平河,点P表示朱河村,点Q表示黄庄村,欲在太平河1上修建一个水泵站(记为点M),分别向两村供水,现有如下四种修建水泵站供水管道的方案,图中实线表示修建的管道,则修建的管道最短的方案是( )| A. | 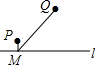 | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.
如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.
如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com