
”¾ĢāÄæ”æŅ»½ŚŹżŃ§æĪŗó£¬ĄĻŹ¦²¼ÖĆĮĖŅ»µĄæĪŗóĮ·Ļ°Ģā£ŗ
ČēĶ¼£¬ŅŃÖŖŌŚRt”÷ABCÖŠ£¬AB=BC£¬”ĻABC=90”ć£¬BO”ĶACÓŚµćO£¬µćP”¢D·Ö±šŌŚAOŗĶBCÉĻ£¬PB=PD£¬DE”ĶACÓŚµćE£¬ĒóÖ¤£ŗ”÷BPO”Õ”÷PDE£®
ĄķĒåĖ¼Ā·£¬±¾ĢāÖ¤Ć÷µÄĖ¼Ā·æÉÓĆĻĀĮŠæņĶ¼±ķŹ¾£ŗ
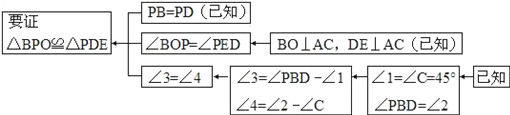
øł¾ŻÉĻŹöĖ¼Ā·£¬ĒėÄćĶź³ÉĻĀĮŠĪŹĢā£®
£Ø1£©ČōBPĘ½·Ö”ĻABO£¬ĘäÓąĢõ¼ž²»±ä£®ĒóÖ¤£ŗAP=CD£®
£Ø2£©ČōµćPŹĒŅ»øö¶Æµć£¬µćPŌĖ¶Æµ½OCµÄÖŠµćP”䏱£¬Āś×ćĢāÖŠĢõ¼žµÄµćDŅ²ĖęÖ®ŌŚÖ±ĻßBCÉĻŌĖ¶Æµ½µćD”䣬ĒėÖ±½ÓŠ“³öCD”äÓėAP”äµÄŹżĮæ¹ŲĻµ,²¢Ö¤Ć÷µĆ³öµÄ¹ŲĻµ.
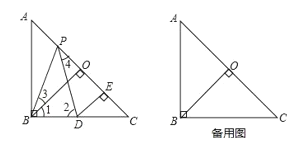
”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£»£Ø2£©CD”ä=![]() AP”䣬ĄķÓɼū½āĪö.
AP”䣬ĄķÓɼū½āĪö.
”¾½āĪö”æ
£Ø1£©ĻČĒó³ö”Ļ3£½”Ļ4£¬ŌŁĒó³ö”ĻABP£½”Ļ4£¬Ēó³ö”÷ABP”Õ”÷CPD£¬¼“æÉµĆ³ö“š°ø£»
£Ø2£©ÉčOP£½CP£½x£¬Ēó³öAP£½3x£¬CD£½![]() x£¬¼“æÉµĆ³ö“š°ø£®
x£¬¼“æÉµĆ³ö“š°ø£®
£Ø1£©Ö¤Ć÷£ŗ
”ßPB£½PD£¬
”ą”Ļ2£½”ĻPBD£¬
”ßAB£½BC£¬”ĻABC£½90”ć£¬
”ą”ĻC£½45”ć£¬
”ßBO”ĶAC£¬
”ą”Ļ1£½45”ć£¬
”ą”Ļ1£½”ĻC£½45”ć£¬
”ß”Ļ3£½”ĻPBC”Ļ1£¬”Ļ4£½”Ļ2”ĻC£¬
”ą”Ļ3£½”Ļ4£¬
”ßBPĘ½·Ö”ĻABO£¬
”ą”ĻABP=”Ļ3£¬
”ą”ĻABP=”Ļ4£¬
ŌŚ”÷ABPŗĶ”÷CPDÖŠ
”ą”÷ABP”Õ”÷CPD£ØAAS£©£¬
”ąAP=CD£®
£Ø2£©½ā£ŗCD”äÓėAP”äµÄŹżĮæ¹ŲĻµŹĒCD”ä=![]() AP”䣮
AP”䣮
ĄķÓÉŹĒ£ŗÉčOP=PC=x£¬ŌņAO=OC=2x=BO£¬
ŌņAP=2x+x=3x£¬
ÓÉ”÷OBP”Õ”÷EPD£¬µĆBO=PE£¬
PE=2x£¬CE=2x©x=x£¬
”ß”ĻE=90”ć£¬”ĻECD=”ĻACB=45”ć£¬
”ąDE=x£¬Óɹ“¹É¶ØĄķµĆ£ŗCD=![]() x£¬
x£¬
¼“AP=3x£¬CD=![]() x£¬
x£¬
”ąCD”äÓėAP”äµÄŹżĮæ¹ŲĻµŹĒCD”ä=![]() AP”ä
APӊ


 ŗģ¹ū×ÓČż¼¶²āŹŌ¾ķĻµĮŠ“š°ø
ŗģ¹ū×ÓČż¼¶²āŹŌ¾ķĻµĮŠ“š°ø æĪĢĆĮ·¼Ó²āĻµĮŠ“š°ø
æĪĢĆĮ·¼Ó²āĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģx2©4![]() x+12+m£½0£®
x+12+m£½0£®
(1)Čō·½³ĢµÄŅ»øöøłŹĒ![]() £¬ĒómµÄÖµ¼°·½³ĢµÄĮķŅ»øł£»
£¬ĒómµÄÖµ¼°·½³ĢµÄĮķŅ»øł£»
(2)Čō·½³ĢµÄĮ½øłĒ”ĪŖµČŃüČż½ĒŠĪµÄĮ½Ńü£¬¶ųÕāøöČż½ĒŠĪµÄµ×±ßĪŖm£¬ĒómµÄÖµ¼°ÕāøöµČŃüČż½ĒŠĪµÄÖܳ¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ”÷ABCµÄČżøö¶„µć×ų±ź·Ö±šŹĒA£Ø1£¬1£©£¬B£Ø4£¬1£©£¬C£Ø3£¬3£©£®
£Ø1£©½«”÷ABCĻņĻĀĘ½ŅĘ5øöµ„Ī»ŗóµĆµ½”÷A1B1C1£¬Ēė»³ö”÷A1B1C1£»
£Ø2£©½«”÷ABCČĘŌµćOÄꏱÕėŠż×Ŗ90”ćŗóµĆµ½”÷A2B2C2£¬Ēė»³ö”÷A2B2C2£»
£Ø3£©ÅŠ¶ĻŅŌO£¬A1£¬BĪŖ¶„µćµÄČż½ĒŠĪµÄŠĪד£®£ØĪŽŠėĖµĆ÷ĄķÓÉ£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
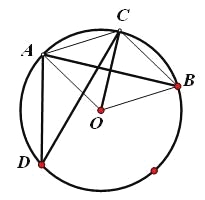
”¾ĢāÄæ”æČēĶ¼£¬µćA”¢B”¢C”¢D¶¼ŌŚ”ŃOÉĻ£¬OC”ĶAB£¬”ĻADC£½30”ć.
£Ø1£©Ēó”ĻBOCµÄ¶ČŹż£»
£Ø2£©ĒóÖ¤£ŗĖıߊĪAOBCŹĒĮāŠĪ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½āĻĀĮŠ²»µČŹ½£Ø×飩
£Ø1£©![]()
£Ø2£©![]()
£Ø3£©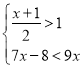 £Ø²¢ŌŚŹżÖįÉĻ±ķŹ¾³ö½ā¼Æ £©
£Ø²¢ŌŚŹżÖįÉĻ±ķŹ¾³ö½ā¼Æ £©
£Ø4£©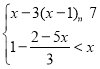 £Ø½ā²»µČŹ½×é²¢Š“³öÕūŹż½ā£©
£Ø½ā²»µČŹ½×é²¢Š“³öÕūŹż½ā£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠŅ»æéŠĪדČēĶ¼µÄĪå±ßŠĪÓąĮĻ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() .ŅŖŌŚÕāæéÓąĮĻÖŠ½ŲČ”Ņ»æé¾ŲŠĪ²ÄĮĻ£¬ĘäÖŠŅ»±ßŌŚ
.ŅŖŌŚÕāæéÓąĮĻÖŠ½ŲČ”Ņ»æé¾ŲŠĪ²ÄĮĻ£¬ĘäÖŠŅ»±ßŌŚ![]() ÉĻ£¬²¢Ź¹Ėł½Ų¾ŲŠĪµÄĆ껿¾”æÉÄÜ“ó.
ÉĻ£¬²¢Ź¹Ėł½Ų¾ŲŠĪµÄĆ껿¾”æÉÄÜ“ó.
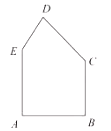
£Ø1£©ČōĖł½Ų¾ŲŠĪ²ÄĮĻµÄŅ»Ģõ±ßŹĒ![]() »ņ
»ņ![]() £¬Ēó¾ŲŠĪ²ÄĮĻµÄĆ껿£»
£¬Ēó¾ŲŠĪ²ÄĮĻµÄĆ껿£»
£Ø2£©ÄÜ·ń½Ų³ö±Č£Ø1£©ÖŠĆ껿øü“óµÄ¾ŲŠĪ²ÄĮĻ£æČē¹ūÄÜ£¬Ēó³öÕāŠ©¾ŲŠĪ²ÄĮĻĆ껿µÄ×ī“óÖµ£¬Čē¹ū²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
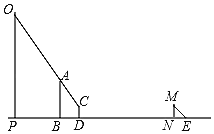
”¾ĢāÄæ”æČēĶ¼£¬Š¦Š¦ŗĶ°Ö°ÖĻėŅŖ²āĮæÖ±Į¢ŌŚµŲĆęÉĻµÄ½ØÖžĪļOPÓė¹ćøęÅĘABµÄøß¶Č£®Ź×ĻČ£¬Š¦Š¦Õ¾ŌŚĄė¹ćøęÅĘB“¦4Ć×µÄD“¦æ“µ½¹ćøęÅĘABµÄ¶„¶ĖA”¢½ØÖžĪļOPµÄ¶„¶ĖOŅ»ĢõÖ±ĻßÉĻ£»“ĖŹ±£¬ŌŚŃō¹āĻĀ£¬°Ö°ÖÕ¾ŌŚN“¦£¬ĖūµÄÓ°³¤NE£½2.1Ć×£¬Ķ¬Ņ»Ź±æĢ£¬²āµĆ½ØÖžĪļOPµÄÓ°³¤ĪŖPG£½28Ć×£¬ŅŃÖŖ½ØÖžĪļOPÓė¹ćøęÅĘABÖ®¼äµÄĖ®Ę½¾ąĄėĪŖ11Ć×£¬Š¦Š¦µÄŃŪ¾¦µ½µŲĆęµÄ¾ąĄėCD£½1.5Ć×£¬°Ö°ÖµÄÉķøßMN£½1.8Ć×£®
£Ø1£©ĒėÄć»³ö±ķŹ¾½ØÖžĪļOPŌŚŃō¹āĻĀµÄÓ°×ÓPG£»
£Ø2£©Ēó£ŗ¢Ł½ØÖžĪļOPµÄøß¶Č£»
¢Ś¹ćøęÅĘABµÄøß¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔ĄöŗĶøēøēŠ”Ć÷·Ö±š“Ó¼ŅŗĶĶ¼Źé¹ŻĶ¬Ź±³ö·¢£¬ŃŲĶ¬Ņ»ĢõĀ·ĻąĻņ¶ųŠŠ£¬Š”ĄöæŖŹ¼Åܲ½£¬Óöµ½øēøēŗóøÄĪŖ²½ŠŠ£¬µ½“ļĶ¼Źé¹ŻĒ”ŗĆÓĆ35·ÖÖÓ£¬Š”Ć÷ŌČĖŁĘļ×ŌŠŠ³µÖ±½Ó»Ų¼Ņ£¬ĘļŠŠ10·ÖÖÓŗóÓöµ½ĮĖĆĆ£¬ŌŁ¼ĢŠųĘļŠŠ5·ÖÖÓ£¬µ½¼ŅĮ½ČĖ¾ąĄė¼ŅµÄĀ·³Ģy£Øm£©Óėø÷×ŌĄėæŖ³ö·¢µÄŹ±¼äx£Ømin£©Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£ŗ
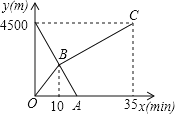
£Ø1£©ĒóĮ½ČĖĻąÓöŹ±Š”Ć÷Ąė¼ŅµÄ¾ąĄė£»
£Ø2£©Ē󊔥öĄė¾ąĄėĶ¼Źé¹Ż500mŹ±ĖłÓƵď±¼ä£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖABŹĒ”ŃOµÄÖ±¾¶£¬µćMŌŚBAµÄŃÓ³¤ĻßÉĻ£¬MDĒŠ”ŃOÓŚµćD£¬¹żµćB×÷BN”ĶMDÓŚµćC£¬Į¬½ÓAD²¢ŃÓ³¤£¬½»BNÓŚµćN£®
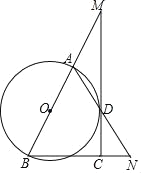
£Ø1£©ĒóÖ¤£ŗAB=BN£»
£Ø2£©ČōMD=4,CD=2.4£¬Ēó![]() ”£
ӣ
£Ø3£©ČōAM=2£¬CN=1.2,Ēó”ŃOµÄ°ė¾¶³¤”£
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com