Question

20．如图，已知矩形纸片ABCD，AB=4，BC=10，M是BC的中点，点P沿折线BA-AD运动，以MP为折痕将矩形纸片向右翻折，使点B落在矩形的边上，则折痕MP的长$\frac{5}{2}\sqrt{5}$或2$\sqrt{5}$或4．

Answer 1

分析 分三种情况进行讨论：①点B′落在AB边上，②点B′落在AD边上，③点B′与点C重合，根据折叠的性质，分别画出图形进行求解．

解答 解：①如图，当点B′落在AB边上时，过M作ME⊥AD于E，可得四边形ABME为矩形，
∴EM=AB=4，AE=BM，
又∵BC=10，M为BC的中点，
∴由折叠可得：B′M=BM=AE=5，
在Rt△EMB′中，根据勾股定理得：B′E=$\sqrt{{5}^{2}-{4}^{2}}$=3，
∴AB′=AE-B′E=2，
设BP=x，则AP=4-x，PB′=x，
在Rt△PAB′中，根据勾股定理得：PB′²=AP²+AB′²，
即x²=（4-x）²+2²，
解得x=$\frac{5}{2}$，
∴PB=$\frac{5}{2}$，
在Rt△BMP中，根据勾股定理得：PM=$\sqrt{（\frac{5}{2}）^{2}+{5}^{2}}$=$\frac{5}{2}\sqrt{5}$；

②如图，当点B′落在AD边上时，过M作ME⊥AD于E，可得四边形ABME为矩形，
∴EM=AB=4，
又∵BC=10，M为BC的中点，
∴由折叠可得：B′M=BM=5，
在Rt△EMB′中，根据勾股定理得：B′E=$\sqrt{{5}^{2}-{4}^{2}}$=3，
由AD∥BC可得，∠DPM=∠BMP，
由折叠可得，∠PMB′=∠BMP，
∴∠DPM=∠PMB′，
∴B′M=B′P=5，
∴PE=5-3=2，
在Rt△PEM中，根据勾股定理得：PM=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$；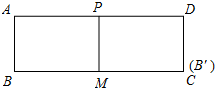

③如图，当点B′与点C重合时，由∠A=∠B=∠BMP=90°，可得四边形ABMP为矩形，
此时，PM=AB=4．
综上所述，折痕MP的长为：$\frac{5}{2}\sqrt{5}$或2$\sqrt{5}$或4．
故答案为：$\frac{5}{2}\sqrt{5}$或2$\sqrt{5}$或4

点评 本题主要考查了轴对称的性质，翻折变换（折叠问题）实质上就是轴对称变换，需要注意折叠前后图形的对应边相等、对应角相等．解题时，常常设要求的线段长为x，然后根据折叠和轴对称的性质，用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．