
��1����ͼ1���ڵȱߡ�ABC�У���M�DZ�BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ�����ȱߡ�AMN������CN����֤����ABC=��ACN��
�����̽����
��2����ͼ2���ڵȱߡ�ABC�У���M�DZ�BC�ӳ����ϵ�����һ�㣨�����˵�C���������������䣬��1���н��ۡ�ABC=��ACN����������˵�����ɣ�
����չ���졿
��3����ͼ3���ڵ�����ABC�У�BA=BC����M�DZ�BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ����������AMN��ʹ���ǡ�AMN=��ABC������CN����̽����ABC���ACN��������ϵ����˵�����ɣ�
 xkb1.com
xkb1.com

w w w .x k b 1.c o m
��1��֤�����ߡ�ABC����AMN�ǵȱ������Σ�
��AB=AC��AM=AN����BAC=��MAN=60�㣬���BAM=��CAN��
���BAM�ա�CAN��SAS����
���ABC=��ACN��
��2�����ۡ�ABC=��ACN�Գ�����
�������£��ߡ�ABC����AMN�ǵȱ������Σ���AB=AC��AM=AN��
��BAC=��MAN=60�㣬���BAM=��CAN��
���BAM�ա�CAN��SAS����
���ABC=��ACN��
��3����ABC=��ACN��
�������£���BA=BC��MA=MN�����ǡ�ABC=��AMN��
��ǡ�BAC=��MAN�����ABC�ס�AMN��
��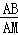 =
=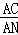 ���֡ߡ�BAM=��BAC����MAC����CAN=��MAN����MAC��
���֡ߡ�BAM=��BAC����MAC����CAN=��MAN����MAC��
���BAM=��CAN�����BAM�ס�CAN��
���ABC=��ACN��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��1��12��ʮ������Ȼ������ȡһ����ȡ������ǡ����4�ı����ĸ�����
| A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��1����֪���κ��� �����㻯��
�����㻯�� ����ʽ������ֱ������ϵ�л���
����ʽ������ֱ������ϵ�л��� ��ͼ��
��ͼ��
��2����� ��
�� �ǣ�1����ͼ���ϵ����㣬��
�ǣ�1����ͼ���ϵ����㣬�� ����ֱ��д��
����ֱ��д�� ��
�� �Ĵ�С��ϵ��
�Ĵ�С��ϵ��
��3�����ã�1���е�ͼ���ʾ������ �ĸ�����Ҫ������ͼ�ۼ���˵�������
�ĸ�����Ҫ������ͼ�ۼ���˵�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��Բ��B��y��ĸ������ϣ��뾶Ϊ5�ġ�B��y��������ύ�ڵ�A��0��1��.����P��0����7����ֱ��l���B�ཻ��C��D���㣬����CD�������п��ܵ�����ֵ��_______���������� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڡ�ABC�У���C=90�㣬ADƽ�֡�CAB��BC�ڵ�D��AB=10��AC=6����D��AB�ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�������ڴ���װ�г���ɫ��ͬ����������ȫ��ͬ��С�����а���2��������3��������5���������ǽ��Ⱥ�Ӵ����������1��������������ĸ����� �� ��
A��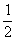 ���� B��
���� B�� �� C��
�� C��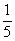 �� D��
�� D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��AB�ǰ�ԲO��ֱ����AB=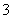
 ����AC=
����AC=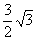 ����PΪ��ԲO��һ�㣨�����A��
����PΪ��ԲO��һ�㣨�����A��
C���غ�. ���APC�Ķ���Ϊ����  ��.
��.
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�Ѷ���ʽx4һ8x2+16�ֽ���ʽ�����ý����( ) ��ԭ����
A��(x-2)2 (x+2)2 B. (x-4)2 (x+4)2 C��(xһ4)2 D��(x-4)4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ����֪���κ���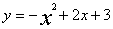 ��������ֱ���A��D��B���㣬����ΪC����ԭ����
��������ֱ���A��D��B���㣬����ΪC����ԭ����
��1����tan��BAC
��2����y�����Ƿ����һ��P��ʹ�á�DOP���ABC���ƣ�������ڣ������P�����꣬��������ڣ�˵�����ɡ�
��3��Q����������һ���㣬ʹ����A��B��C��QΪ�˵���ı�����һ�����Σ���ֱ��д������������Q������ꡣ����Ҫ��д��������̣�
 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com