
【题目】已知,反比例函数![]() 的图象过第二象限内的点
的图象过第二象限内的点![]() ,
,![]() 轴于
轴于![]() ,
,![]() 面积为3,若直线
面积为3,若直线![]() 经过点
经过点![]() ,并且经过反比例函数
,并且经过反比例函数![]() 的图象上另一点
的图象上另一点![]() .
.
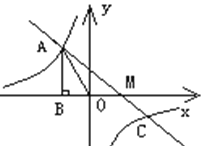
(1)求反比例函数的解析式;
(2)求直线![]() 解析式
解析式
(3)求![]() 的面积;
的面积;
(4)直接写出不等式![]() 的解集.
的解集.
【答案】(1)反比例函数为![]() ;(2)直线
;(2)直线![]() 的解析式为:
的解析式为:![]() ;(3)
;(3)![]() 的面积
的面积![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据Rt△AOB面积为得到a=3,则A点坐标为(2,3),把A点坐标代入![]() 可得k=2×3=6,确定反比例函数的解析式为
可得k=2×3=6,确定反比例函数的解析式为![]() ;;
;;
(2)把C点坐标代入反比例函数的解析式![]() 可确定C点坐标为
可确定C点坐标为![]() ,然后利用待定系数法确定经过A点和C点的直线解析式;
,然后利用待定系数法确定经过A点和C点的直线解析式;
(3)先求出M点的坐标,然后利用S△AOC=S△AOM+S△COM进行计算即可;
(4)由A、C两点的坐标可直接得出不等式的解集.
(1)∵![]() 面积为3,
面积为3,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵反比例函数为![]() 过点
过点![]() ,
,
∴![]() ,即反比例函数为:
,即反比例函数为:![]() ,
,
∵反比例函数为![]() ,
,
(2)∵点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]()
∴![]() .
.
∵直线![]() 经过点
经过点![]()
∴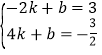
解得: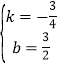
∴直线![]() 的解析式为:
的解析式为:![]() .
.
(3)连OC,
对于![]() ,令y=0,则
,令y=0,则![]() ,解得x=2,
,解得x=2,
∴M点的坐标为(2,0),
∴S△AOC=S△AOM+S△COM=![]() ×2×3+
×2×3+![]() ×2×
×2×![]() =
=![]() ;
;
(4)∵A(2,3),C(4,![]() ),
),
∴由函数图象可知,不等式![]() 的解集是x≤2或0<x≤4.
的解集是x≤2或0<x≤4.



 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5吨,5辆大货车与6辆小货车一次可以运货35吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现在租用这两种货车共10辆,要求一次运输货物不低于30吨,则大货车至少租几辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的位置如图所示.点A,B,C的坐标分别为
的位置如图所示.点A,B,C的坐标分别为![]() ,
,![]() ,
,![]() ,根据下面要求完成解答.
,根据下面要求完成解答.

(1)作![]() 关于点C成中心对称的
关于点C成中心对称的![]() ;
;
(2)将![]() 向右平移4个单位,作出平移后的
向右平移4个单位,作出平移后的![]() ;
;
(3)在x轴上求作一点P,使![]() 的值最小,直接写出点P的坐标.
的值最小,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月,小军顺利升入初中,为学习需要,准备购买若干个创意笔记本,甲、乙两家文具店都有足够数量的创意笔记本,这两家文具店创意笔记本标价都是每个8元,甲文具店的销售方案是:购买创意笔记本的数量不超过6个时,原价销售;购买创意笔记本超过6个时,从第7个开始按标价的![]() 出售;乙文具店的销售方案是:不管购买多少个创意笔记本,一律按标价的
出售;乙文具店的销售方案是:不管购买多少个创意笔记本,一律按标价的![]() 出售.
出售.
(1)若设小军要购买![]() 个创意笔记本,请用含
个创意笔记本,请用含![]() 的代数式分别表示小军到甲文具店和乙文具店购买全部创意笔记本所需的费用;
的代数式分别表示小军到甲文具店和乙文具店购买全部创意笔记本所需的费用;
(2)小军购买多少个创意笔记本时,到甲、乙两家文具店购买全部创意笔记本所需的费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 过点
过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 过点
过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.
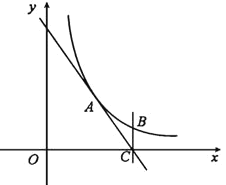
(1)求![]() 的值与
的值与![]() 点的坐标;
点的坐标;
(2)连结![]() ,求
,求![]() 的面积;
的面积;
(3)在平面内有点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形为平行四边形,试写出符合条件的所有
四点为顶点的四边形为平行四边形,试写出符合条件的所有![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
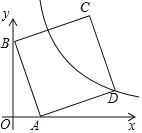
【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线y=![]() 上;将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是_____.
上;将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
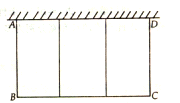
【题目】李老伯想用24米长的旧木料,靠![]() 米长的围墙造一个如图所示的猪舍,它们的平面图是一排大小相等的三个长方形,总面积为32平方米.
米长的围墙造一个如图所示的猪舍,它们的平面图是一排大小相等的三个长方形,总面积为32平方米.
(1)求猪舍的长BC和宽AB各为多少米?
(2)题中围墙的长度![]() 米对猪舍的长和宽是否有影响?怎样影响?
米对猪舍的长和宽是否有影响?怎样影响?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com