
【题目】如图,一次函数y1=kx+b的图象与x轴、y轴分别交于点A、B,与一次函数y2=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D. 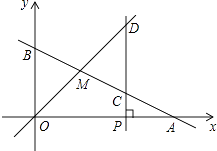
(1)求一次函数y1=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值.
【答案】
(1)解:∵M的横坐标为2,点M在直线y=x上,
∴y=2,
∴M(2,2)
把M(2,2)、A(6,0)代入y1=kx+b中,
可得: ![]() ,
,
解得: 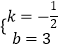
∴函数的表达式为:y1=﹣ ![]() x+3
x+3
(2)解:∵PD⊥x轴,
∴PC∥OB
∴∠BOM=∠CDM,
∵点M是线段CD的中点,
∴MO=MD
在△MBO与△MCD中
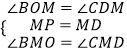
∴△MBO≌△MCD(ASA)
∴OB=CD
当x=0时,
y1= ![]() x+3=3,
x+3=3,
∴OB=2,
∴DC=3,
当x=a时,
y1=﹣ ![]() x+3=3﹣
x+3=3﹣ ![]() a,
a,
∴y2=x=a
即D(a,a),C(a,﹣ ![]() a+3)
a+3)
∴DC=a﹣(﹣ ![]() a+3)=
a+3)= ![]() a﹣3=3,
a﹣3=3,
∴a=4
【解析】(1)先求出M的坐标,然后将M与A的坐标代入y1=kx+b中,即可求出k与b的值.(2)根据条件先证明△MBO≌△MCD(ASA),由此可知OB=CD,分别求出OB与CD的长度即可求出a的值.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】下列所给的条件中,能确定相似的有( )
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个;B.4个;C.5个;D.6个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的括号里:
﹣8,0.275, ![]() ,0,﹣1.04,﹣(﹣3),﹣
,0,﹣1.04,﹣(﹣3),﹣ ![]() ,|﹣2|
,|﹣2|
正数集合{…}
负整数集合{…}
分数集合{…}
负数集合{…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件羽绒服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利250元.若设这件羽绒服的成本是x元,根据题意,可得到的方程是( )
A.x(1+50%)×80%=x﹣250
B.x(1+50%)×80%=x+250
C.(1+50%x)×80%=x﹣250
D.(1+50%x)×80%=250﹣x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“朋友三角形”.
性质:“朋友三角形”的面积相等.
如图1,在△ABC中,CD是AB边上的中线.
那么△ACD和△BCD是“朋友三角形”,并且S△ACD=S△BCD .
应用:如图2,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=AD=4,BC=6,点E在BC上,点F在AD上,BE=AF,AE与BF交于点O.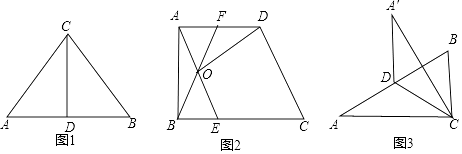
(1)求证:△AOB和△AOF是“朋友三角形”;
(2)连接OD,若△AOF和△DOF是“朋友三角形”,求四边形CDOE的面积.
拓展:如图3,在△ABC中,∠A=30°,AB=8,点D在线段AB上,连接CD,△ACD和△BCD是“朋友三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的 ![]() ,则△ABC的面积是(请直接写出答案).
,则△ABC的面积是(请直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com