
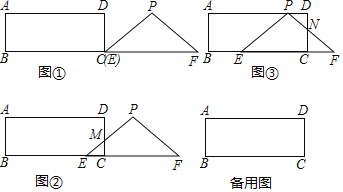
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点C与点E重合),点B,C(E),F在同一直线上,AB=3cm,BC=9cm,EF=8cm,PE=PF=5cm,如图②,△EFP从图①的位置出发,沿CB方向匀速运动,速度为2cm/s,当点F与点C重合时△EFP停止运动停止.设运动时间为t(s)(0<t<4),解答下列问题:
(1)当0<t<2时,EP与CD交于点M,请用含t的代数式表示CE=______,CM=______;
(2)当2<t<4时,如图③,PF与CD交于点N,设四边形EPNC的面积为y(cm2),求y与t之间的函数关系式;
(3)当2<t<4时,且S四边形EPNC:S矩形ABCD=1:4时,请求出t的值;
(4)连接BD,在运动过程中,当BD与EP相交时,设交点为O,当t=______时;O在∠BAD的平分线上.(不需要写解答过程)
【答案】(1)2t , t ;(2)y=-![]() t2+12t-12;(3)t=4 -
t2+12t-12;(3)t=4 -![]() ;(4)
;(4)![]() .
.
【解析】
(1)由等腰三角形的性质可得PH=3cm,EH=HF=4cm,由题意可得EC=2t,由锐角三角形函数可得tan∠PEH=![]() ,可得MC=
,可得MC=![]() t;
t;
(2)由锐角三角函数可得CN=![]() ,由S△PEF-S△CNF=S四边形EPNC,可求y与t之间的函数关系式;
,由S△PEF-S△CNF=S四边形EPNC,可求y与t之间的函数关系式;
(3)由题意可得y=![]() ,代入解析式可求t的值;
,代入解析式可求t的值;
(4)过点O作OM⊥AD,ON⊥AB,垂足分别为点M,点N,可得四边形ANOM是矩形,可得AM=ON,由角平分线的性质可得OM=ON,由三角形的面积关系可得ON=OM=![]() =AM,由锐角三角函数和平行线分线段成比例可求EC的长,即可求t的值.
=AM,由锐角三角函数和平行线分线段成比例可求EC的长,即可求t的值.
解:(1)如图,过点P作PH⊥EF,垂足为H,
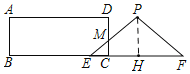
∵EF=8cm,PE=PF=5cm,PH⊥EF,
∴EH=HF=4cm,
∴PH=![]() =3cm,
=3cm,
∵△EFP沿CB方向匀速运动,速度为2cm/s,
∴CE=2t,
∵tan∠PEH=![]()
∴![]()
∴MC=![]() t,
t,
故答案为:2t,![]() t,
t,
(2)如图,过点P作PH⊥BC于点H,
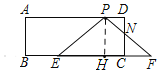
由(1)可知:PH=3cm,EH=HF=4cm,
∴S△PEF=![]() ×8×3=12,
×8×3=12,
∵CF=EF-EC,
∴CF=8-2t,
∵tan∠PFE=![]() ,
,
∴CN=![]() ,
,
∴y=S△PEF-S△CNF=12-![]() ×(8-2t)×
×(8-2t)×![]() (8-2t)=-
(8-2t)=-![]() t2+12t-12
t2+12t-12
(3)∵S四边形EPNC:S矩形ABCD=1:4
∴![]() ×3×9=-
×3×9=-![]() t2+12t-12
t2+12t-12
∴2t2-16t+25=0
∴t=4±![]()
∵2<t<4
∴t=4-![]()
(4)如图,过点O作OM⊥AD,ON⊥AB,垂足分别为点M,点N,
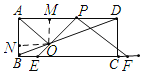
∵OM⊥AD,ON⊥AB,∠BAD=90°,
∴四边形ANOM是矩形,
∴AM=ON,
∵AO平分∠DAB,OM⊥AD,ON⊥AB,
∴OM=ON,
∵S△ABD=S△ABO+S△AOD,
∴![]()
∴ON=OM=![]() =AM,
=AM,
∵AD∥BC
∴∠APE=∠PEC
∵tan∠APE=tan∠PEC=![]() =
=![]()
∴MP=3,
∴PD=AD-AM-MP=![]()
∵ON∥AD
∴![]()
∴![]()
∵AD∥BC
∴![]()
∴BE=![]() PD=
PD=![]()
∴EC=BC-EB=![]()
∴t=![]() =
=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】关于x的方程(x-3)(x-5)=m(m>0)有两个实数根![]() ,
,![]() (
( ![]() <
<![]() ),则下列选项正确的是( )
),则下列选项正确的是( )
A. 3<![]() <
<![]() <5 B. 3<
<5 B. 3<![]() <5<
<5<![]() C.
C. ![]() <2<
<2<![]() <5 D.
<5 D. ![]() <3且
<3且![]() >5
>5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在倡导学生大课间活动中,随机抽取了部分学生对“我最喜爱课间活动”进行了一次抽样调查,分别从打篮球、踢足球、自由活动、跳绳、其它、等5个方面进行问卷调查(每人只能选一项),根据调查结果绘制了如图的不完整统计图,请你根据图中信息,解答下列问题
(1)本次调查共抽取了学生多少人?
(2)求本次调查中喜欢踢足球人数,并补全条形统计图;
(3)若全校共有中学生1200人,请你估计我校喜欢跳绳学生有多少人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.
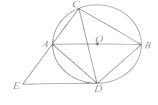
(1)△ABD的面积是________:
(2)求证:DE是⊙O的切线:
(3)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
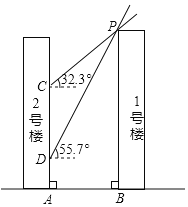
【题目】如图,1号楼在2号楼的南侧,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=35m.请求出两楼之间的距离AB的长度(结果保留整数)
(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个全等的直角三角形ABC和DBE按图![]() 方式摆放,其中
方式摆放,其中![]() ,
,![]() ,点E落在AB上,DE所在直线交AC所在直线于点F.
,点E落在AB上,DE所在直线交AC所在直线于点F.
![]() 求证:
求证:![]() ;
;
![]() 若将图
若将图![]() 中的
中的![]() 绕点B按顺时针方向旋转角a,且
绕点B按顺时针方向旋转角a,且![]() ,其他条件不变,如图
,其他条件不变,如图![]() 请你直接写出
请你直接写出![]() 与DE的大小关系:
与DE的大小关系:![]() ______
______![]() 填“
填“![]() ”或“
”或“![]() ”或“
”或“![]() ”
”![]()
![]() 若将图
若将图![]() 中
中![]() 的绕点B按顺时针方向旋转角
的绕点B按顺时针方向旋转角![]() ,且
,且![]() ,其他条件不变,如图
,其他条件不变,如图![]() 请你写出此时AF、EF与DE之间的关系,并加以证明.
请你写出此时AF、EF与DE之间的关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
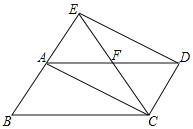
【题目】如图,将ABCD沿其对角线AC折叠,使△ABC落在AEC处,CE与AD交于点F,连接DE.
(1)请你判断AC,DE的位置关系,并说明理由;
(2)若折叠后,CE平分AD,AB=4,BC=6,请利用(1)中的结论,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
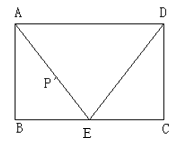
【题目】已知矩形![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 为
为![]() 中点,动点
中点,动点![]() 以2米/秒的速度从
以2米/秒的速度从![]() 出发,沿着
出发,沿着![]() 的边,按照A
的边,按照A![]() E
E![]() D
D![]() A顺序环行一周,设
A顺序环行一周,设![]() 从
从![]() 出发经过
出发经过![]() 秒后,
秒后,![]() 的面积为
的面积为![]() (平方米),求
(平方米),求![]() 与
与![]() 间的函数关系式.
间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
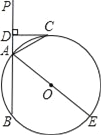
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com