
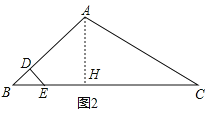
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.

【答案】(1)最短的斜拉索DE的长为3![]() m;(2)最长的斜拉索AC的长为30m.
m;(2)最长的斜拉索AC的长为30m.
【解析】(1)根据等腰直角三角形的性质计算DE的长;
(2)作AH⊥BC于H,如图2,由于BD=DE=3![]() ,则AB=3BD=15
,则AB=3BD=15![]() ,在Rt△ABH中,根据等腰直角三角形的性质可计算出BH=AH=15,然后在Rt△ACH中利用含30度的直角三角形三边的关系即可得到AC的长.
,在Rt△ABH中,根据等腰直角三角形的性质可计算出BH=AH=15,然后在Rt△ACH中利用含30度的直角三角形三边的关系即可得到AC的长.
(1)∵∠ABC=∠DEB=45°,
∴△BDE为等腰直角三角形,
∴DE=![]() BE=
BE=![]() ×6=3
×6=3![]() ,
,
答:最短的斜拉索DE的长为3![]() m;
m;
(2)作AH⊥BC于H,如图2,
∵BD=DE=3![]() ,
,
∴AB=3BD=5×3![]() =15
=15![]() ,
,
在Rt△ABH中,∵∠B=45°,
∴BH=AH=![]() AB=
AB=![]() ×15
×15![]() =15,
=15,
在Rt△ACH中,∵∠C=30°,
∴AC=2AH=30.
答:最长的斜拉索AC的长为30m.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】对于每个正整数![]() ,设
,设![]() 表示
表示![]() 的末位数字.例如:
的末位数字.例如:![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),…则
的末位数字),…则![]() 的值为( )
的值为( )
A.4040B.4038C.0D.4042
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE//BC,分别交AB,AC于点D,E,若AB=4,AC=3,则△ADE的周长是_______________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=5,BC=CD且BC>AB,BD=8.给出以下判断:
①AC垂直平分BD;
②四边形ABCD的面积S=ACBD;
③顺次连接四边形ABCD的四边中点得到的四边形可能是正方形;
④当A,B,C,D四点在同一个圆上时,该圆的半径为![]() ;
;
⑤将△ABD沿直线BD对折,点A落在点E处,连接BE并延长交CD于点F,当BF⊥CD时,点F到直线AB的距离为![]() .
.
其中正确的是_____.(写出所有正确判断的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题:
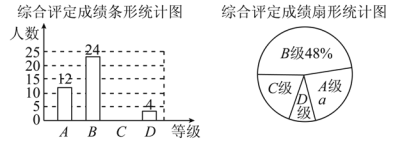
(1)在这次调查中,一共抽取了________名学生,a=________%;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为________度;
(4)若该校共有2 000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:对于关于x的一次函数y=kx+b(k≠0),我们称函数y=![]() 为一次函数y=kx+b(k≠0)的m变函数(其中m为常数).
为一次函数y=kx+b(k≠0)的m变函数(其中m为常数).
例如:对于关于x的一次函数y=x+4的3变函数为y=![]()
(1)关于x的一次函数y=-x+1的2变函数为![]() ,则当x=4时,
,则当x=4时,![]() = ;
= ;
(2)关于x的一次函数y=x+2的1变函数为![]() ,关于x的一次函数y=-
,关于x的一次函数y=-![]() x-2的-1变函数为
x-2的-1变函数为![]() ,求函数
,求函数![]() 和函数
和函数![]() 的交点坐标;
的交点坐标;
(3)关于x的一次函数y=2x+2的1变函数为![]() ,关于x的一次函数y=
,关于x的一次函数y=![]() x-1,的m变函数为
x-1,的m变函数为![]() .
.
①当-3≤x≤3时,函数![]() 的取值范围是 (直接写出答案):
的取值范围是 (直接写出答案):
②若函数![]() 和函数
和函数![]() 有且仅有两个交点,则m的取值范围是 (直接写出答案).
有且仅有两个交点,则m的取值范围是 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点0,过点0的直线分别交边AD,BC于点E,F,EF=6.则AE2+BF2的值为( )
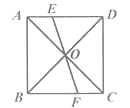
A. 9 B. 16 C. 18 D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
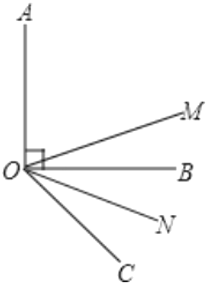
【题目】如图,已知![]() 与
与![]() 互为余角,且
互为余角,且![]() 平分
平分![]() 平分
平分![]() .
.
(1)求![]() 的度数;
的度数;
(2)如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;如果已知
_______度;如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;
_______度;
(3)从以上求![]() 的过程中,你得出的结论是__________.
的过程中,你得出的结论是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com