
【题目】为了参加中考体育测试,甲,乙,丙三位同学进行足球传球训练.球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求请用树状图列举出三次传球的所有可能情况;
(2)传球三次后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到丙脚下的概率大?
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧![]() 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
(1)求证:OE=![]() AC;
AC;
(2)求证:![]() ;
;
(3)当AC=6,AB=10时,求切线PC的长.
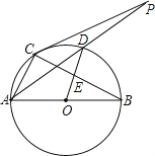
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个正整数x的首位数字与末位数字先立方再求和得到一个新数(若x<10,则直接将x立方得到新数),定义为M(x)运算.例如:M(2)=23=8,M(31)=33+13=28,M(102)=13+23=9,规定对某个正整数x进行第一次M(x)运算记作M1(x),第二次M(x)运算记作M2(x),……,第n次M(x)运算记作Mn(x),例如:M1(2)=23=8,M2(2)=83=512,M3(2)=53+23=133.
(1)求M2(3)和M2017(3);
(2)若M5n(3)=520,求正整数n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知△ABC中AB=AC,∠BAC=36°,BD是角平分线,求证:点D是线段AC的黄金分割点;
(2)如图2,正五边形的边长为2,连结对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,求MN的长;
(3)设⊙O的半径为r,直接写出它的内接正十边形的长=_________________(用r的代数式表示).
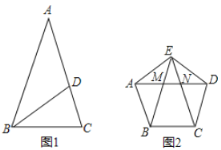
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(﹣5,0),B(﹣3,0)点C在y的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°,点P从点A出发,沿x轴向右以每秒1个单位长度的速度运动,运动时间为t秒.
(1)当时t=1,求PC的长;
(2)当∠BCP=15°时,求t的值;
(3)以线段PC为直径的⊙Q随点P的运动而变化,当⊙Q与四边形ABCD的边(或边所在的直线)相切时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点.三角形ABC的三个顶点均在格点上,以点A为圆心的弧EF与BC相切于格点D,分别交AB,AC于点E,F.
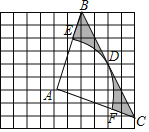
(1)直接写出三角形ABC边长AB= ;AC= ;BC= .
(2)求图中由线段EB,BC,CF及弧FE所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度,2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2013年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2013年底共建设了多少万平方米廉租房.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com