
ЁОЬтФПЁПЪЕбщгыВйзїЃК
аЁУїЪЧвЛЮЛЖЏЪжФмСІКмЧПЕФЭЌбЇЃЌЫћгУЯ№ЦЄФрзіГЩвЛИіРтГЄЮЊ![]() ЕФе§ЗНЬхЃЎ
ЕФе§ЗНЬхЃЎ
![]() ШчЭМ
ШчЭМ![]() ЫљЪОЃЌдкЖЅУцжааФЮЛжУДІДгЩЯЕНЯТДђвЛИіБпГЄЮЊ
ЫљЪОЃЌдкЖЅУцжааФЮЛжУДІДгЩЯЕНЯТДђвЛИіБпГЄЮЊ![]() ЕФе§ЗНаЮПзЃЌДђПзКѓЕФЯ№ЦЄФрПщЕФБэУцЛ§ЮЊ________
ЕФе§ЗНаЮПзЃЌДђПзКѓЕФЯ№ЦЄФрПщЕФБэУцЛ§ЮЊ________![]() ЃЛ
ЃЛ
![]() ШчЙћдкЕк
ШчЙћдкЕк![]() ЬтДђПзКѓЃЌдйдке§УцжааФЮЛжУЃЈШчЭМ
ЬтДђПзКѓЃЌдйдке§УцжааФЮЛжУЃЈШчЭМ![]() жаЕФащЯпЫљЪОЃЉДгЧАЕНКѓДђвЛИіБпГЄЮЊ
жаЕФащЯпЫљЪОЃЉДгЧАЕНКѓДђвЛИіБпГЄЮЊ![]() ЕФе§ЗНаЮЭЈПзЃЌФЧУДДђПзКѓЕФЯ№ЦЄФрПщЕФБэУцЛ§ЮЊ________
ЕФе§ЗНаЮЭЈПзЃЌФЧУДДђПзКѓЕФЯ№ЦЄФрПщЕФБэУцЛ§ЮЊ________![]() ЃЛ
ЃЛ
![]() ШчЙћАб
ШчЙћАб![]() ЁЂ
ЁЂ![]() жаЕФБпГЄЮЊ
жаЕФБпГЄЮЊ![]() ЕФЭЈПзОљИФЮЊБпГЄЮЊ
ЕФЭЈПзОљИФЮЊБпГЄЮЊ![]() ЕФЭЈПзЃЌФмЗёЪЙЯ№ЦЄФрПщЕФБэУцЛ§ЮЊ
ЕФЭЈПзЃЌФмЗёЪЙЯ№ЦЄФрПщЕФБэУцЛ§ЮЊ![]() ЃПШчЙћФмЃЌЧѓГі
ЃПШчЙћФмЃЌЧѓГі![]() ЃЌШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЃЌШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ110ЃЛЃЈ2ЃЉ118ЃЛЃЈ3ЃЉЕББпГЄИФЮЊ![]() ЪБЃЌБэУцЛ§ЮЊ
ЪБЃЌБэУцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉДђПзКѓЕФБэУцЛ§=де§ЗНЬхЕФБэУцЛ§ЉаЁе§ЗНаЮПзЕФУцЛ§+ПзжаЕФЫФИіОиаЮЕФУцЛ§ЃЎ
ЃЈ2ЃЉДђПзКѓЕФБэУцЛ§=ЭМЂйжаЕФБэУцЛ§Љ2ИіаЁе§ЗНаЮПзЕФУцЛ§+аТДђЕФПзжаЕФАЫИіаЁОиаЮЕФУцЛ§ЃЎ
ЃЈ3ЃЉИљОнЃЈ1ЃЉЃЈ2ЃЉжаЕФУцЛ§МЦЫуЗНЗЈЃЌгУaБэЪОГіЭМЂйКЭЭМЂкЕФУцЛ§ЃЎШЛКѓШУгУЕУГіЕФЭМЂкЕФБэУцЛ§=118МЦЫуГіaЕФжЕЃЎ
ЃЈ1ЃЉБэУцЛ§S1=96Љ2+4ЁС4=110ЃЈcm2ЃЉЃЎ
ЙЪД№АИЮЊЃК110ЃЛ
ЃЈ2ЃЉБэУцЛ§S2=S1Љ4+4ЁС1.5ЁС2=118ЃЈcm2ЃЉЃЎ
ЙЪД№АИЮЊЃК118ЃЛ
ЃЈ3ЃЉФмЪЙЯ№ЦЄФрПщЕФБэУцЛ§ЮЊ118cm2ЃЌРэгЩЮЊЃК
ЁпS1=96Љ2a2+4aЁС4ЃЌS2=S1Љ4a2+4ЁС4aЉ4a2
Ёр96Љ2a2+16aЉ8a2+16a=118
ЁЁ96Љ10a2+32a=118
5a2Љ16a+11=0
Ёрa1=![]() ЃЌa2=1
ЃЌa2=1
ЁпaЁй1ЃЌ![]() ЃМ4
ЃМ4
ЁрЕББпГЄИФЮЊ![]() cmЪБЃЌБэУцЛ§ЮЊ118cm2ЃЎ
cmЪБЃЌБэУцЛ§ЮЊ118cm2ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЗжБ№ЪЧФГАрШЋЬхбЇЩњЩЯбЇЪБГЫГЕЁЂВНааЁЂЦяГЕШЫЪ§ЕФЗжВМжБЗНЭМКЭЩШаЮЭГМЦЭМЃЈСНЭМЖМВЛЭъећЃЉЃЌЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉ

A. ИУАрзмШЫЪ§ЮЊ50ШЫB. ВНааШЫЪ§ЮЊ30ШЫ
C. ГЫГЕШЫЪ§ЪЧЦяГЕШЫЪ§ЕФ2.5БЖD. ЦяГЕШЫЪ§еМ20%
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпy=x2Љ6x+9гыжБЯпy=x+3НЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЌжБЯпy=x+3гыxжсНЛгкЕуDЃЎ
ЃЈЂёЃЉЧѓХзЮяЯпЕФЖЅЕуCЕФзјБъМАAЃЌBСНЕуЕФзјБъЃЛ
ЃЈЂђЃЉНЋХзЮяЯпy=x2Љ6x+9ЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌдйЯђзѓЦНвЦtЃЈtЃО0ЃЉИіЕЅЮЛГЄЖШЕУЕНаТХзЮяЯпЃЌШєаТХзЮяЯпЕФЖЅЕуEдкЁїDACФкЃЌЧѓtЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉЕуPЃЈmЃЌnЃЉЃЈЉ3ЃМmЃМ1ЃЉЪЧХзЮяЯпy=x2Љ6x+9ЩЯвЛЕуЃЌЕБЁїPABЕФУцЛ§ЪЧЁїABCУцЛ§ЕФ2БЖЪБЃЌЧѓmЃЌnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁгБЭЌбЇбЇЭъЭГМЦжЊЪЖКѓЃЌЫцЛњЕїВщСЫЫ§ЫљдкЯНЧјШєИЩУћОгУёЕФФъСфЃЌНЋЕїВщЪ§ОнЛцжЦГЩШчЯТЩШаЮКЭЬѕаЮЭГМЦЭМЃК

ЧыИљОнвдЩЯВЛЭъећЕФЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаЁгБЭЌбЇЙВЕїВщСЫЖрЩйУћОгУёЕФФъСфЃЌЩШаЮЭГМЦЭМжаaЃЌbИїЕШгкЖрЩйЃП
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУЯНЧјФъСфдк0ЁЋ14ЫъЕФОгУёдМга1500ШЫЃЌЧыЙРМЦФъСфдк15ЁЋ59ЫъЕФОгУёЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГАрЁА2016ФъСЊЛЖЛсЁБжаЃЌгавЛИіУўНБгЮЯЗЃКга4еХжНХЦЃЌБГУцЖМЪЧЯВбђбђЭЗЯёЃЌе§Уцга2еХЪЧаІСГЃЌ2еХЪЧПоСГЃЌЯжНЋ4еХжНХЦЯДдШКѓБГУцГЏЩЯАкЗХЕНзРЩЯЃЌШЛКѓШУЭЌбЇШЅЗжНХЦЃЎ
ЃЈ1ЃЉЯждкаЁЗМКЭаЁЯМЗжБ№гавЛДЮЗХЦЛњЛсЃЌШєе§УцЪЧаІСГЃЌдђаЁЗМЛёНБЃЛШєе§УцЪЧПоСГЃЌдђаЁЯМЛёНБЃЌЫ§УЧЛёНБЕФЛњЛсЯрЭЌТ№ЃПХаЖЯВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШчЙћаЁЗМЁЂаЁУїЖМгаЗСНеХХЦЕФЛњЛсЃЎЗХЦЙцдђЃКаЁЗМЯШЗвЛеХЃЌЗХЛиКѓдйЗвЛеХЃЛаЁУїЭЌЪБЗПЊСНеХжНХЦЃЎЫћУЧЗПЊЕФСНеХжНХЦжажЛвЊГіЯжаІСГОЭЛёНБЃЎЧыЮЪЫћУЧЛёНБЕФЛњЛсЯрЕШТ№ЃПХаЖЯВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаИіОљдШЕФе§ЪЎЖўУцЬхЕФїЛзгЃЌЦфжа1ИіУцБъгаЁА1ЁБЃЌ2ИіУцБъгаЁА2ЁБЃЌ3ИіУцБъгаЁА3ЁБЃЌ2ИіУцБъгаЁА4ЁБЃЌ1ИіУцБъгаЁА5ЁБЃЌЦфгрУцБъгаЁА6ЁБЃЌНЋетИіїЛзгжРГіКѓЃК
(1)жРГіЁА6ЁБГЏЩЯЕФПЩФмадгаЖрДѓЃП
(2)ФФаЉЪ§зжГЏЩЯЕФПЩФмадвЛбљДѓЃП
(3)ФФаЉЪ§зжГЏЩЯЕФПЩФмадзюДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
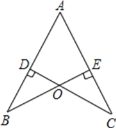
ЁОЬтФПЁПШчЭМЃЌвбжЊABЃНACЃЌCDЁЭABгкDЃЌBEЁЭACгкEЃЌBEгыCDЯрНЛгкЕуOЃЎ
ЃЈ1ЃЉЮЪЬтЬНОПЃКЯпЖЮOBЃЌOCгаКЮЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЮЪЬтЭиеЙЃКЗжБ№СЌНгOAЃЌBCЃЌЪдХаЖЯжБЯпOAЃЌBCЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЮЪЬтбгЩьЃКНЋЬтФПЬѕМўжаЕФЁАCDЁЭABгкDЃЌBEЁЭACгкEЁБЛЛГЩЁАDЁЂEЗжБ№ЮЊABЃЌACБпЩЯЕФжаЕуЁБЃЌЃЈ1ЃЉЃЈ2ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПЧыжБНгаДГіНсТлЃЌВЛБиЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+cЕФЖЅЕузјБъЮЊPЃЈ2ЃЌ9ЃЉЃЌгыxжсНЛгкЕуAЃЌBЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ5ЃЉЃЎ
ЃЈЂёЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНМАЕуAЃЌBЕФзјБъЃЛ
ЃЈЂђЃЉЩшЕуQдкЕквЛЯѓЯоЕФХзЮяЯпЩЯЃЌШєЦфЙигкдЕуЕФЖдГЦЕуQЁфвВдкХзЮяЯпЩЯЃЌЧѓЕуQЕФзјБъЃЛ
ЃЈЂѓЃЉШєЕуMдкХзЮяЯпЩЯЃЌЕуNдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЪЙЕУвдAЃЌCЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧвACЮЊЦфвЛБпЃЌЧѓЕуMЃЌNЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com