
【题目】为预防疾病,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量![]() (mg)与燃烧时间
(mg)与燃烧时间![]() (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后, ![]() 与
与![]() 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时![]() 与
与![]() 的函数关系式.(2)求药物燃烧后
的函数关系式.(2)求药物燃烧后![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】(1)小My同学在网络直播课中学习了勾股定理,他想把这一知识应用在等边三角形中:边长为a的等边三角形面积是 (用含a的代数式表示);
(2)小My同学进一步思考:是否可以将正方形剪拼成一个等边三角形(不重叠、无缝隙)?
①如果将一个边长为2的正方形纸片剪拼等边三角形,那么该三角形边长的平方是 ;
②小My同学按下图切割方法将正方形ABCD剪拼成一个等边三角形EFG:M、N分别为AB、CD边上的中点,P、Q是边BC、AD上两点,G为MQ上一点,且∠MGP=∠PGN=∠NGQ=60°.
请补全图形,画出拼成正三角形的各部分分割线,并标号;
③正方形ABCD的边长为2,设BP=x,则x2= .

查看答案和解析>>
科目:初中数学 来源: 题型:
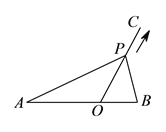
【题目】如图,点![]() 在线段
在线段![]() 上,
上, ![]() ,
, ![]() ,
, ![]() 为射线,且
为射线,且![]() ,动点
,动点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,沿射线
出发,沿射线![]() 做匀速运动,设运动时间为
做匀速运动,设运动时间为![]() 妙.
妙.
(![]() )当
)当![]() 秒时,则
秒时,则![]() __________,
__________, ![]() __________.
__________.
(![]() )当
)当![]() 是直角三角形时,求
是直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
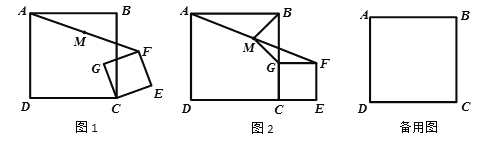
【题目】如图1,正方形CEFG绕正方形ABCD的顶点C旋转,连接AF,点M是AF中点.
(1)当点G在BC上时,如图2,连接BM、MG,求证:BM=MG;
(2)在旋转过程中,当点B、G、F三点在同一直线上,若AB=5,CE=3,则MF= ;
(3)在旋转过程中,当点G在对角线AC上时,连接DG、MG,请你画出图形,探究DG、MG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)﹣(﹣2)+(﹣4);
(2)﹣10+14+16﹣8;
(3)(-4)×(-5)-90÷(-15);
(4)﹣23÷![]() ×(﹣
×(﹣![]() )2;
)2;
(5)(![]() +
+![]() ﹣
﹣![]() )×(﹣36);
)×(﹣36);
(6)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com